Câu hỏi:
25/08/2024 5,655
Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí A trên mặt nước và rơi trở lại mặt nước ở vị trí B, đường đi của nước có dạng một phần của parabol \(y = - \frac{1}{4}{x^2}\) trong hệ trục toạ độ Oxy, với gốc tọa độ O là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục Ox song song với AB, x và y được tính theo đơn vị mét. Tính chiều cao h từ điểm O đến mặt nước, biết khoảng cách giữa điểm A và điểm B là 6 m.
Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí A trên mặt nước và rơi trở lại mặt nước ở vị trí B, đường đi của nước có dạng một phần của parabol \(y = - \frac{1}{4}{x^2}\) trong hệ trục toạ độ Oxy, với gốc tọa độ O là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục Ox song song với AB, x và y được tính theo đơn vị mét. Tính chiều cao h từ điểm O đến mặt nước, biết khoảng cách giữa điểm A và điểm B là 6 m.
Quảng cáo
Trả lời:
Giải bởi Vietjack
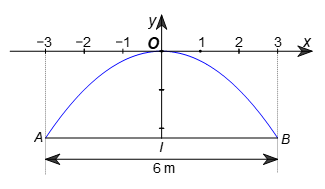
Gọi I là trung điểm của đoạn AB. Khi đó OI = h và \(AI = IB = \frac{{AB}}{2} = \frac{6}{2} = 3\,\,\left( {\rm{m}} \right).\)
Từ đó, trong hệ trục Oxy, hoành độ của B bằng 3, tung độ của B bằng –h.
Do đó: \( - h = - \frac{1}{4} \cdot {3^2}\) hay \( - h = \frac{{ - 9}}{4},\) suy ra \(h = \frac{9}{4} = 2,25\,\,\left( {\rm{m}} \right).\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
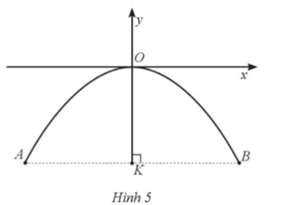
Từ Hình 5, ta có K(0; –4,5).
Gọi hoành độ của điểm B là b (b > 0).
Do tung độ của điểm B bằng tung độ của K nên B(b; –4,5).
Mặt khác, B thuộc parabol \(y = - \frac{1}{8}{x^2}\) nên ta có:
\( - 4,5 = - \frac{1}{8}{b^2}\) hay b2 = 36, nên b = 6 (do b > 0).
Từ đó KB = 6 m và AB = 2.KB = 2.6 = 12 m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất bằng 12 mét.
Lời giải
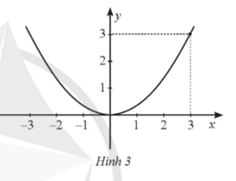
Với t = 3, y = 2,25 ta có: 2,25 = a.32 nên a = 0,25.
Với a = 0,25 ta có: y = 0,25t2. (1)
Thay y = 6,25 vào (1) ta được: 6,25 = 0,25t2. (2)
Từ (2) và t > 0, ta có t = 5.
Vậy khi viên bi lăn được 6,25 m thì nó đã lăn trong 5 giây.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận