Câu hỏi:
06/09/2024 1,505
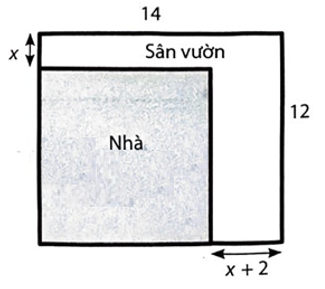
Trên một khu vườn hình vuông có cạnh bằng 20 m người ta làm một lối đi xung quanh vườn có bề rộng x (m) (Hình dưới). Để diện tích lối đi là 76 m2 thì bề rộng x là bao nhiêu?
Trên một khu vườn hình vuông có cạnh bằng 20 m người ta làm một lối đi xung quanh vườn có bề rộng x (m) (Hình dưới). Để diện tích lối đi là 76 m2 thì bề rộng x là bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phần đất làm vườn là hình vuông có cạnh 20 – 2x (m) và có diện tích là (20 – 2x)2 (m2).
Theo giả thiết, diện tích đất dành cho làm vườn là 202 – 76 = 400 – 76 = 324 suy ra (20 – 2x)2 = 324 = 182 hay (20 – 2x)2 – 182 = 0 (1).
Giải phương trình (1): (20 – 2x)2 – 182 = 0
(20 – 2x – 18)(20 – 2x + 18) = 0
(2 – 2x)(38 – 2x) = 0.
Suy ra 2 – 2x = 0 hoặc 38 – 2x = 0.
• 2 – 2x = 0 hay 2x = 2, suy ra x = 1.
• 38 – 2x = 0 hay 2x = 38, suy ra x = 19 (loại vì 20 – 2.19 = −18 < 0).
Vậy bề rộng của lối đi là 1 m.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có (x2 – 4) + x(x – 2) = 0
(x – 2)(x + 2) + x(x – 2) = 0
(x – 2)(x + 2 + x) = 0
(x – 2)(2x + 2) = 0
Ta giải phương trình sau:
• x – 2 = 0 hay x = 2.
• 2x + 2 hay 2x = −2, suy ra x = −1.
Vậy phương trình có hai nghiệm là: x = −1 và x = 2.
b) Ta có (2x + 1)2 – 9x2 = 0
(2x + 1)2 – (3x)2 = 0
(2x + 1 – 3x)(2x + 1 + 3x) = 0
(1 – x)(5x + 1) = 0
Suy ra 1 – x = 0 hoặc 5x + 1 = 0.
Ta giải hai phương trình:
• 1 – x = 0 hay x = 1.
• 5x + 1 = 0 hay 5x = −1, suy ra \(x = - \frac{1}{5}.\)
Vậy phương trình có hai nghiệm x = 1 và \(x = - \frac{1}{5}.\)
Lời giải
a) Ta có x(x – 2) = 0
Nên x = 0 hoặc x – 2 = 0
x = 0 hoặc x = 2
Vậy phương trình đã cho có nghiệm là x = 0 và x = 2.
b) Ta có (2x + 1)(3x – 2) = 0
Nên 2x + 1 = 0 hoặc 3x – 2 = 0.
• 2x + 1 = 0 hay 2x = −1, suy ra \(x = - \frac{1}{2}.\)
• 3x – 2 = 0 hay 3x = 2, suy ra \(x = \frac{2}{3}.\)
Vậy phương trình đã cho có nghiệm là \(x = - \frac{1}{2}\) và \(x = \frac{2}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận