Câu hỏi:
15/09/2024 1,670
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.30).
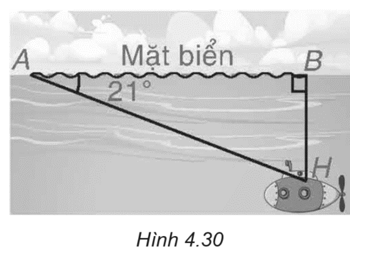
a) Khi tàu chuyển động theo hướng đo và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (Làm tròn đến m).
b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.30).
a) Khi tàu chuyển động theo hướng đo và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (Làm tròn đến m).
b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Độ sâu cần tính là đoạn BH.
Trong tam giác ABH, ta có
\(h = BH = AH.\sin A = 200.\sin 21^\circ \approx 72\) (m).
b) Đổi 9 km = 9 000 m.
Để lặn được 9 000 m, tàu cần 60 phút.
Để lặn sâu 1 m, tài cần \(\frac{{60}}{{9000}}\) phút. Do đó, để lặn sâu 200 m tàu cần
\(200 \cdot \frac{{60}}{{9\,\,000}} = \frac{{12\,\,000}}{{9\,\,000}} = \frac{4}{3}\) (phút) = 80 (giây).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
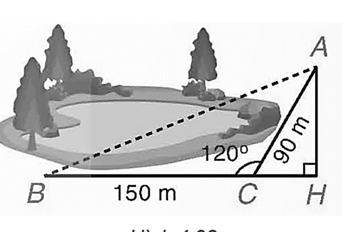
Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.
Trong tam giác ACH, ta có
\(\widehat {ACH} = 180^\circ - 120^\circ = 60^\circ ,\)
\(HC = AC.\cos \widehat {ACH} = 90.\cos 60^\circ = 90.\frac{1}{2} = 45\) (m),
\(AH = AC.\sin \widehat {ACH} = 90.\sin 60^\circ = 90.\frac{{\sqrt 3 }}{2} = 45\sqrt 3 \) (m).
Từ đó BH = BC + HC = 150 + 45 = 195 (m),
\(A{B^2} = A{H^2} + B{H^2} = {\left( {45\sqrt 3 } \right)^2} + {195^2} = 44100\) suy ra \(AB = \sqrt {44100} = 210\) (m).
Vậy AB = 210 m.
Lời giải
(H.4.24)
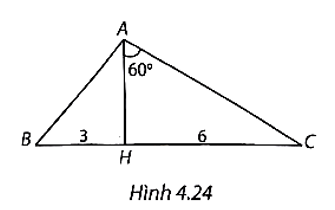
Tam giác ACH vuông tại H, HC = 6 cm, \(\widehat {HAC} = 60^\circ .\)
Trong tam giác vuông AHC, ta có
\(\sin \widehat {HAC} = \frac{{CH}}{{AC}}\) nên \(AC = \frac{{CH}}{{\sin \widehat {HAC}}} = \frac{6}{{\sin 60^\circ }} = \frac{6}{{\frac{{\sqrt 3 }}{2}}} = 4\sqrt 3 \approx 7\) (cm),
\(AH = CH.\cot A = 6.\cot 60^\circ = 6.\frac{{\sqrt 3 }}{3} = 2\sqrt 3 \approx 3\) (cm),
\(\widehat {ACB}\) là góc phụ với \(\widehat {HAC}\) nên \(\widehat {ACB} = 90^\circ - \widehat {HAC} = 90^\circ - 60^\circ = 30^\circ .\)
Trong tam giác vuông AHB, ta có
AB2 = AH2 + BH2 = 32 + 32 = 18 nên \(AB = \sqrt {18} \approx 4\) (cm),
\[\tan B = \frac{{AH}}{{BH}} = \frac{3}{3}\] nên \(\widehat B \approx 45^\circ .\)
Trong tam giác ABC, ta có
\(\widehat {BAC} = 180^\circ - \widehat C - \widehat B = 180^\circ - 30^\circ - 45^\circ \approx 105^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo