Tính các số liệu còn thiếu (dấu “?”) ở Hình 4.26 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
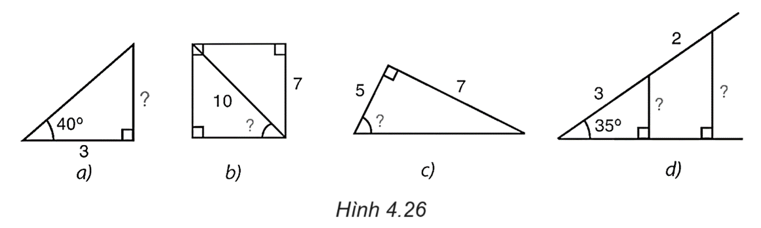
Tính các số liệu còn thiếu (dấu “?”) ở Hình 4.26 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
(H.4.27)
Ta đặt tên các điểm như trong Hình 4.27.
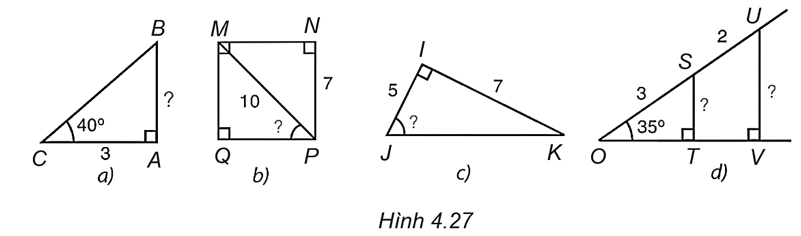
Ở hình a): Trong tam giác ABC vuông tại A, theo định lí về hai cạnh góc vuông, ta có
\(AB = AC.\tan C = 3.\tan 40^\circ \approx 2,5.\)
Ở hình b): Ta có QM = NP = 7.
Trong tam giác MPQ vuông tại Q, ta có
\(\sin \widehat {MPQ} = \frac{{MQ}}{{MP}} = \frac{7}{{10}}\) nên \(\widehat {MPQ} \approx 44^\circ .\)
Ở hình c): Trong tam giác IJK vuông tại I, ta có
\(\tan \widehat {IJK} = \frac{{IK}}{{IJ}} = \frac{7}{5}\) nên \(\widehat {IJK} \approx 54^\circ .\)
Ở hình d): Trong tam giác OST vuông tại T, ta có
\(\sin 35^\circ = \sin \widehat {SOT} = \frac{{ST}}{{SO}}\) nên \(ST = \sin 35^\circ .SO = \sin 35^\circ .3 \approx 1,7\)
Trong tam giác OUV vuông tại V, ta có
OU = OS + SU = 3 + 2 = 5.
\(\sin 35^\circ = \sin \widehat {UOV} = \frac{{UV}}{{OU}}\) nên \(UV = OU.\sin 35^\circ = 5.\sin 35^\circ \approx 2,8.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
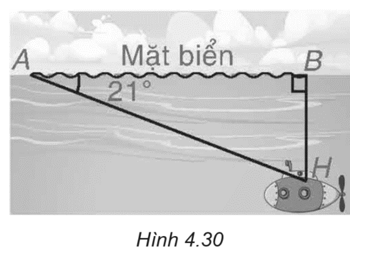
Độ sâu cần tính là đoạn BH.
Trong tam giác ABH, ta có
\(h = BH = AH.\sin A = 200.\sin 21^\circ \approx 72\) (m).
b) Đổi 9 km = 9 000 m.
Để lặn được 9 000 m, tàu cần 60 phút.
Để lặn sâu 1 m, tài cần \(\frac{{60}}{{9000}}\) phút. Do đó, để lặn sâu 200 m tàu cần
\(200 \cdot \frac{{60}}{{9\,\,000}} = \frac{{12\,\,000}}{{9\,\,000}} = \frac{4}{3}\) (phút) = 80 (giây).
Lời giải
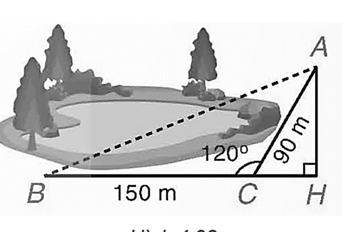
Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.
Trong tam giác ACH, ta có
\(\widehat {ACH} = 180^\circ - 120^\circ = 60^\circ ,\)
\(HC = AC.\cos \widehat {ACH} = 90.\cos 60^\circ = 90.\frac{1}{2} = 45\) (m),
\(AH = AC.\sin \widehat {ACH} = 90.\sin 60^\circ = 90.\frac{{\sqrt 3 }}{2} = 45\sqrt 3 \) (m).
Từ đó BH = BC + HC = 150 + 45 = 195 (m),
\(A{B^2} = A{H^2} + B{H^2} = {\left( {45\sqrt 3 } \right)^2} + {195^2} = 44100\) suy ra \(AB = \sqrt {44100} = 210\) (m).
Vậy AB = 210 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập