Câu hỏi:
15/09/2024 971
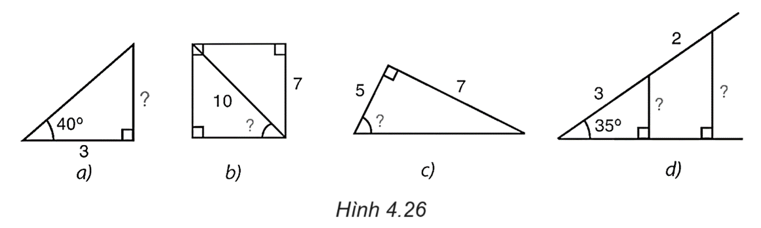
Giải tam giác ABC vuông tại A, biết
a) BC = 20, \(\widehat C = 40^\circ ;\)
b) AC = 82, \(\widehat B = 55^\circ ;\)
c) BC = 32, AC = 20.
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).
Giải tam giác ABC vuông tại A, biết
a) BC = 20, \(\widehat C = 40^\circ ;\)
b) AC = 82, \(\widehat B = 55^\circ ;\)
c) BC = 32, AC = 20.
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) (H.4.31)
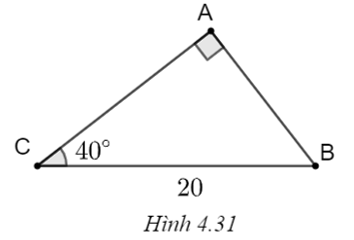
Ta có:
\(\widehat B = 90^\circ - \widehat C = 90^\circ - 40^\circ = 50^\circ ,\)
\(AC = BC.\cos C = 20.\cos 40^\circ \approx 15,3,\)
\(AB = BC.\sin C = 20.\sin 40^\circ \approx 12,8.\)
b) (H.4.32)
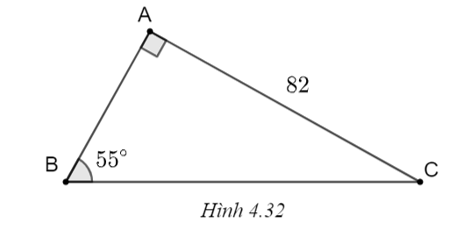
Ta có
\(\widehat C = 90^\circ - \widehat B = 90^\circ - 55^\circ = 35^\circ ,\)
\(AB = AC.\cot B = 82.\cot 55^\circ \approx 57,4,\)
\(B{C^2} = A{B^2} + A{C^2} = {57,4^2} + {82^2} = 10018,76,\) suy ra \(BC = \sqrt {10\,\,018,76} \approx 100,1.\)
c) (H.4.33)
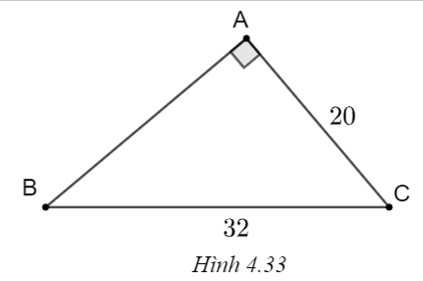
Ta có
\(A{B^2} = B{C^2} - A{C^2} = {32^2} - {20^2} = 624,\) suy ra \(AB = \sqrt {624} \approx 25.\)
\(\sin B = \frac{{AC}}{{BC}} = \frac{{20}}{{32}} = 0,625,\) suy ra \(\widehat B \approx 39^\circ .\)
Từ đó suy ra \(\widehat C = 90^\circ - \widehat B = 90^\circ - 39^\circ = 51^\circ .\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
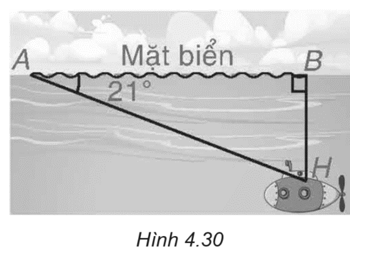
Độ sâu cần tính là đoạn BH.
Trong tam giác ABH, ta có
\(h = BH = AH.\sin A = 200.\sin 21^\circ \approx 72\) (m).
b) Đổi 9 km = 9 000 m.
Để lặn được 9 000 m, tàu cần 60 phút.
Để lặn sâu 1 m, tài cần \(\frac{{60}}{{9000}}\) phút. Do đó, để lặn sâu 200 m tàu cần
\(200 \cdot \frac{{60}}{{9\,\,000}} = \frac{{12\,\,000}}{{9\,\,000}} = \frac{4}{3}\) (phút) = 80 (giây).
Lời giải
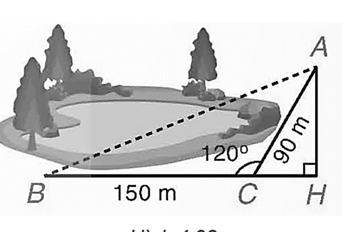
Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.
Trong tam giác ACH, ta có
\(\widehat {ACH} = 180^\circ - 120^\circ = 60^\circ ,\)
\(HC = AC.\cos \widehat {ACH} = 90.\cos 60^\circ = 90.\frac{1}{2} = 45\) (m),
\(AH = AC.\sin \widehat {ACH} = 90.\sin 60^\circ = 90.\frac{{\sqrt 3 }}{2} = 45\sqrt 3 \) (m).
Từ đó BH = BC + HC = 150 + 45 = 195 (m),
\(A{B^2} = A{H^2} + B{H^2} = {\left( {45\sqrt 3 } \right)^2} + {195^2} = 44100\) suy ra \(AB = \sqrt {44100} = 210\) (m).
Vậy AB = 210 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo