Một chủ nhà hàng kinh doanh phần ăn uống đồng giá có chiến lược kinh doanh như sau:
Phí cố định được ước tính trong một năm là 50 000 nghìn đồng.
Chi phí một phần ăn ước tính khoảng 22 nghìn đồng.
Giá niêm yết trên thực đơn là 30 nghìn đồng.
Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu x là số phần ăn tự phục vụ trong một năm, giả sử x thuộc khoảng [5 000; 25 000].
a) Gọi C(x) là tổng chi phí hằng năm cho x phần ăn này. Xác định C(x).
b) Chứng tỏ rằng giá thành của một phần ăn cho bởi biểu thức D(x) = 22 + \(\frac{{50000}}{x}\) (nghìn đồng).
c) Sử dụng đồ thị, hãy xác định điểm hòa vốn của nhà hàng, tức là số lượng phần ăn tối thiểu phải được phục vụ hằng năm để hoạt động của nhà hàng tạo ra lợi nhuận. Hãy chứng minh điều đó.
d) Chứng minh rằng tổng lợi nhuận hằng năm cho x phần ăn được biểu thị bởi:
L(x) = 8x – 50 000 (nghìn đồng).
e) Mục tiêu của chủ nhà hàng là tạo ra lợi nhuận ít nhất là 120 000 nghìn đồng mỗi năm. Biết rằng nhà hàng mở cửa 300 ngày một năm, hỏi trung bình mỗi ngày nhà phàng phải phục vụ ít nhất bao nhiêu phần ăn để đạt được mục tiêu trên.
Một chủ nhà hàng kinh doanh phần ăn uống đồng giá có chiến lược kinh doanh như sau:
Phí cố định được ước tính trong một năm là 50 000 nghìn đồng.
Chi phí một phần ăn ước tính khoảng 22 nghìn đồng.
Giá niêm yết trên thực đơn là 30 nghìn đồng.
Trong bài này, giả định rằng tất cả các phần ăn chế biến sẵn đều được bán hết và kí hiệu x là số phần ăn tự phục vụ trong một năm, giả sử x thuộc khoảng [5 000; 25 000].
a) Gọi C(x) là tổng chi phí hằng năm cho x phần ăn này. Xác định C(x).
b) Chứng tỏ rằng giá thành của một phần ăn cho bởi biểu thức D(x) = 22 + \(\frac{{50000}}{x}\) (nghìn đồng).
c) Sử dụng đồ thị, hãy xác định điểm hòa vốn của nhà hàng, tức là số lượng phần ăn tối thiểu phải được phục vụ hằng năm để hoạt động của nhà hàng tạo ra lợi nhuận. Hãy chứng minh điều đó.
d) Chứng minh rằng tổng lợi nhuận hằng năm cho x phần ăn được biểu thị bởi:
L(x) = 8x – 50 000 (nghìn đồng).
e) Mục tiêu của chủ nhà hàng là tạo ra lợi nhuận ít nhất là 120 000 nghìn đồng mỗi năm. Biết rằng nhà hàng mở cửa 300 ngày một năm, hỏi trung bình mỗi ngày nhà phàng phải phục vụ ít nhất bao nhiêu phần ăn để đạt được mục tiêu trên.
Quảng cáo
Trả lời:
a) Ta có: C(x) = 22x + 50 000 (nghìn đồng).
b) Giá thành một phần ăn là: D(x) = \(\frac{{C(x)}}{x} = 22 + \frac{{50000}}{x}\) nghìn đồng.
c) Xét: \(22 + \frac{{50000}}{x}\) = 30 ⇔ x = 6250.
Ta có đồ thị hàm số:
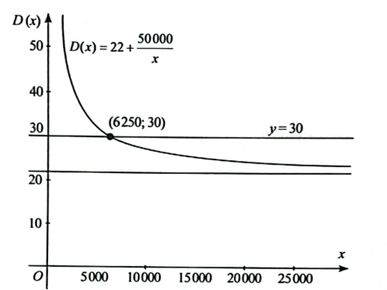
Quan sát đồ thị hàm số, ta thấy giao điểm của đồ thị hàm số D(x) và đường thẳng y = 30 là điểm có tọa độ (6250; 30). Nghĩa là khi phục vụ được tối thiểu 6250 phần ăn thì chi phí một phần ăn bằng tiền bán một phần ăn (là 30 nghìn đồng).
Đồ thị cũng cho thấy rằng nếu phục vụ ít hơn 6250 phần ăn thì chi phí cho 1 phần ăn cao hơn giá 1 phần ăn, nghĩa là nhà hàng sẽ lỗ.
Như vậy điểm hòa vốn là 6250.
d) Tổng lợi nhuận hằng năm cho x phần ăn là
L(x) = 30x – (22x + 50 000) = 8x – 50 000 (nghìn đồng).
e) Để đạt mục tiêu lợi nhuận hằng năm ít nhất là 120 000 nghìn đồng thì số phần ăn cần bán được phải thỏa mãn bất phương trình sau:
L(x) ≥ 120 000
⇔ 8x – 50 000 ≥ 120 000
⇔ x ≥ 21 250.
Kết quả cho thấy hằng năm, nhà hàng cần phục vụ được tối thiểu 21 250 phần ăn thì mới có lợi nhuận như mong muốn.
Do nhà hàng mở cửa 300 ngày một năm nên trung bình mỗi ngày nhà hàng cần phục vụ số phần ăn là:
21 250 : 300 ≈ 70,8 phần ăn.
Vậy để đạt mục tiêu, trung bình mỗi ngày nhà hàng cần phục vụ ít nhất 71 phần ăn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lợi nhuận xưởng thu được trong một ngày khi sản xuất x (kg) thành phẩm là:
P(x) = 513x – (2x3 – 30x2 + 177x + 2 592) = −2x3 + 30x2 + 336x – 2 592 với 0 ≤ x ≤ 20.
Ta có: P'(x) = −6x2 + 60x + 336
P'(x) = 0 ⇔ x = 14 hoặc x = −4 (loại do −4 ∉ [0; 20]).
Ta có bảng biến thiên:
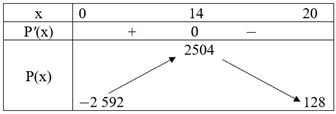
Do đó \(\mathop {\max }\limits_{\left[ {0;20} \right]} P\left( x \right) = P\left( {14} \right) = 2504\).
Vậy x = 14 kg.
Lời giải
Ta có: h(t) = \( - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\) với 0 ≤ t ≤ 20.
h'(t) = \( - \frac{{12}}{{255}}{t^2} + \frac{{98}}{{85}}{t^2} - \frac{{98}}{{17}}\)
h'(t) = 0 ⇔ x = 7 hoặc x = \(\frac{{37}}{5}\).
Bảng xét dấu:

Do đó, tàu lượn đi xuống khi t trong các khoảng (0; 7) và \(\left( {\frac{{37}}{5};20} \right)\), tàu lượn đi lên khi t trong khoảng \(\left( {7;\frac{{37}}{5}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.