Giải SBT Toán 12 Chân trời sáng tạo Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án

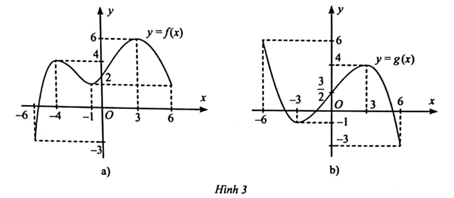
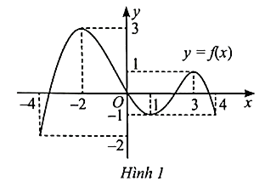
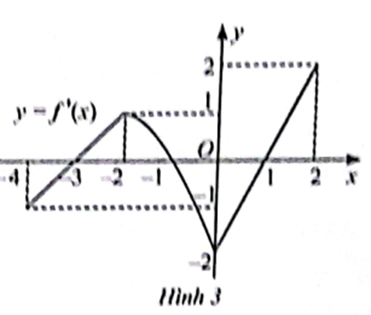
a) Dựa vào đồ thị hàm số, ta thấy:

Hàm số đồng biến trên các khoảng (−6; −4) và (−1; 3).

Hàm số nghịch biết trên các khoảng (−4; −1) và (3; 6).

Hàm số đạt cực đại tại x = −4, y_CĐ = 4 và tại x = 3, y_CĐ = 6.

Hàm số đạt cực tiểu tại x = −1, y_CT = 2.

b) Dựa vào đồ thị hàm số, ta thấy:

Hàm số đồng biến trên khoảng (−3; 3).

Hàm số nghịch biến trên các khoảng (−6; −3) và (3; 6).

Hàm số đạt cực đại tại x = 3, y_CĐ = 4.

Hàm số đạt cực tiểu tại x = −3, y_CT = −1.

a) y = −x³ – 3x² + 24x – 1

Tập xác định: D = ℝ.

Ta có: y' = −3x² – 6x + 24 ⇔ y' = 0 ⇔ x = 2 hoặc x = −4.

Ta có bảng biến thiên như sau:

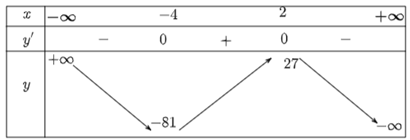
Hàm số đồng biến trên khoảng (−4; 2).

Hàm số nghịch biến trên các khoảng (−∞; −4) và (2; +∞).

Hàm số đạt cực đại tại x = 2, y_CĐ = 27.

Hàm số đạt cực tiểu tại x = −4, y_CT = −81.

b) y = x³ – 8x² + 5x + 2

Tập xác định: D = ℝ.

Ta có: y' = 3x² – 16x + 5 ⇔ y' = 0 ⇔ x = 5 hoặc x = \(\frac{1}{3}\).

Ta có bảng biến thiên:

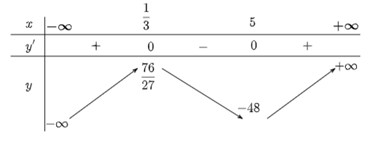
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và (5; +∞).

Hàm số nghịch biến trên khoảng \(\left( {\frac{1}{3};5} \right)\).

Hàm số đạt cực đại tại x = \(\frac{1}{3}\), y_CĐ = \(\frac{{76}}{{27}}\).

Hàm số đạt cực tiểu tại x = 5, y_CT = −48.

c) y = x³ + 2x² + 3x + 1

Tập xác định: D = ℝ.

Ta có: y' = 3x² + 4x + 3 = \(3{\left( {x + \frac{2}{3}} \right)^2} + \frac{5}{3}\) > 0, với mọi x.

Do đó hàm số đồng biến trên (−∞; +∞).

Hàm số không có cực trị.

d) y = −3x³ + 3x² – x + 2.

Tập xác định: D = ℝ.

Ta có: y' = −9x² + 6x – 1 = −(3x – 1)² ≤ 0, với mọi x.

Do đó, hàm số nghịch biến trên (−∞; +∞).

Hàm số không có cực trị.

a) \(y = \frac{{3x + 1}}{{x - 2}}\)

Tập xác định: D = ℝ\{2}.

Ta có: y' = \(\frac{{ - 7}}{{{{\left( {x - 2} \right)}^2}}}\) < 0, với mọi x ∈ D.

Bảng biến thiên:

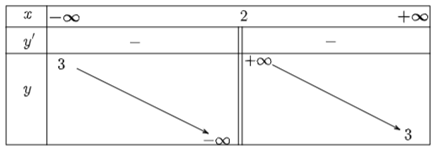
Do đó, hàm nghịch biến trên các khoảng (−∞; 2) và (2; +∞).

Hàm số không có cực trị.

b) \(y = \frac{{2x - 5}}{{3x + 1}}\)

Tập xác định: D = ℝ\\(\left\{ {\frac{{ - 1}}{3}} \right\}\).

Ta có: y' = \(\frac{{10}}{{{{\left( {3x + 1} \right)}^2}}}\) > 0, với mọi x ∈ D.

Bảng biến thiên:

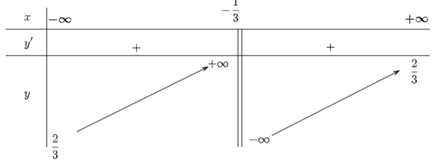
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;\frac{{ - 1}}{3}} \right)\) và \(\left( { - \frac{1}{3}; + \infty } \right)\).

Hàm số không có cực trị.

c) \(y = \sqrt {4 - {x^2}} \)

Tập xác định: D = [−2; 2].

Ta có: y' = \(\frac{{ - x}}{{\sqrt {4 - {x^2}} }}\) ⇔ y' = 0 ⇔ x = 0.

Ta có bảng biến thiên như sau:

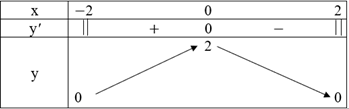
Hàm số đồng biến trên khoảng (−2; 0) và nghịch biến trên khoảng (0; 2).

Hàm số đạt cực đại tại x = 0, y_CĐ = 2.

d) \(y = x - \ln x\)

Tập xác định: D = (0; +∞).

Ta có: y' = 1 – \(\frac{1}{x}\) = \(\frac{{x - 1}}{x}\) ⇔ y' = 0 ⇔ x = 1.

Ta có bảng biến thiên như sau:

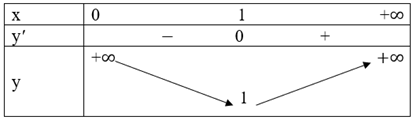
Hàm số đồng biến trên khoảng (1; +∞).

Hàm số nghịch biến trên khoảng (0; 1).

Hàm số đạt cực tiểu tại x = 1, y_CT = 1.

a) \(y = \frac{{{x^2} + 8}}{{x + 1}}\)

Tập xác định: D = ℝ\{−1}.

Ta có: y' = \(\frac{{2x\left( {x + 1} \right) - {x^2} - 8}}{{{{\left( {x + 1} \right)}^2}}}\) = \(\frac{{{x^2} + 2x - 8}}{{{{\left( {x + 1} \right)}^2}}}\)

           y' = 0 ⇔ x² + 2x – 8 = 0 ⇔ x = 2 hoặc x = −4.

Ta có bảng biến thiên:

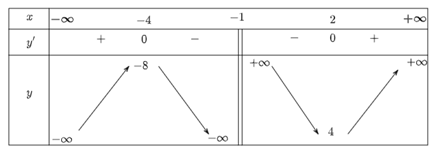
Hàm số đồng biến trên các khoảng (−∞; −4) và (2; +∞).

Hàm số nghịch biến trên các khoảng (−4; −1) và (−1; 2).

Hàm số đạt cực đại tại x = −4, y_CĐ = −8.

Hàm số đạt cực tiểu tại x = 2, y_CT = 4.

b) \(y = \frac{{{x^2} - 8x + 10}}{{x - 2}}\)

Tập xác định: D = ℝ\{2}.

Ta có: y' = \(\frac{{\left( {2x - 8} \right)\left( {x - 2} \right) - {x^2} + 8x - 10}}{{{{\left( {x - 2} \right)}^2}}}\) = \(\frac{{{x^2} - 4x + 6}}{{{{\left( {x - 2} \right)}^2}}}\) = \(\frac{{{{\left( {x - 2} \right)}^2} + 2}}{{{{\left( {x - 2} \right)}^2}}}\) .

Nhận thấy y' > 0, với mọi x ∈ D.

Ta có bảng biến thiên như sau:

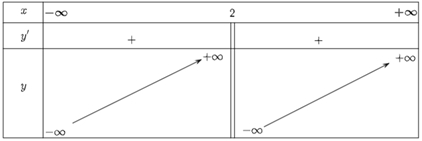
Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞).

Hàm số không có cực trị.

c) \(y = \frac{{ - 2{x^2} + x + 2}}{{2x - 1}}\)

Tập xác định: D = ℝ\\(\left\{ {\frac{1}{2}} \right\}\).

Ta có: y' = \(\frac{{\left( { - 4x + 1} \right)\left( {2x - 1} \right) - 2\left( { - 2{x^2} + x + 2} \right)}}{{{{\left( {2x - 1} \right)}^2}}}\) = \(\frac{{ - 4{x^2} + 4x - 5}}{{{{\left( {2x - 1} \right)}^2}}}\)= \(\frac{{{{\left( {2x - 1} \right)}^2} - 6}}{{{{\left( {2x - 1} \right)}^2}}}\)

Nhận thấy y' < 0, với mọi x ∈ D.

Ta có bảng biến thiên:

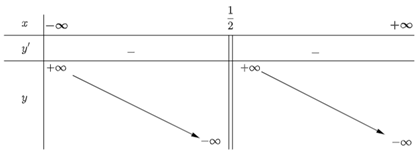
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;\frac{1}{2}} \right)\) và \(\left( {\frac{1}{2}; + \infty } \right)\).

Hàm số không có cực trị.

d) \(y = \frac{{ - {x^2} - 6x - 25}}{{x + 3}}.\)

Tập xác định: D = ℝ\{−3}.

Ta có: y' =\(\frac{{\left( { - 2x - 6} \right)\left( {x + 3} \right) + {x^2} + 6x + 25}}{{{{\left( {x + 3} \right)}^2}}}\) = \(\frac{{ - {x^2} - 6x + 7}}{{{{\left( {x + 3} \right)}^2}}}\)

           y' = 0 ⇔ \(\frac{{ - {x^2} - 6x + 7}}{{{{\left( {x + 3} \right)}^2}}}\) = 0 ⇔ x = 1 hoặc x = −7.

Bảng biến thiên:

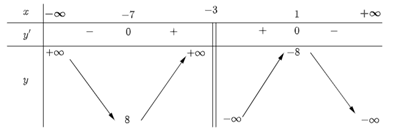
Hàm số đồng biến trên các khoảng (−7; −3) và (−3; 1).

Hàm số nghịch biến trên các khoảng (−∞; −7) và (1; +∞).

Hàm số đạt cực đại tại x = 1, y_CĐ = −8.

Hàm số đạt cực tiểu tại x = −7, y_CT = 8.

a) \(y = \frac{{2x + m}}{{x - 1}}\)

Tập xác định: D = ℝ\{1}.

Ta có: y' = \(\frac{{ - 2 - m}}{{{{\left( {x - 1} \right)}^2}}}\).

Để hàm số đồng biến trên từng khoảng xác định

⇔ y' = \(\frac{{ - 2 - m}}{{{{\left( {x - 1} \right)}^2}}}\) > 0 với mọi x ∈ ℝ\{1}.

⇔ −2 – m > 0

⇔ m < −2.

b) \(y = \frac{{ - {x^2} + 3x + m}}{{x + 2}}\)

Tập xác định: D = ℝ\{−2}.

Ta có: y' = \(\frac{{\left( { - 2x + 3} \right)\left( {x + 2} \right) + {x^2} - 3x - m}}{{{{\left( {x + 2} \right)}^2}}}\) = \(\frac{{ - {x^2} - 4x + 6 - m}}{{{{\left( {x + 2} \right)}^2}}}\)

Để hàm số nghịch biến trên từng khoảng xác định

y' ≤ 0 với mọi x ∈ ℝ\{−2}.

⇔ −x2 – 4x + 6 – m ≤ 0 với mọi x ∈ ℝ\{−2}.

⇔ ∆' = 4 + 6 – m ≤ 0

⇔ 10 – m ≤ 0

⇔ m ≥ 10.

Từ đồ thị hàm số y = f'(x) trên, ta có bảng xét dấu sau:

Hàm số y = f(x) đồng biến trên các khoảng (−3; −2) và (1; 2), hàm số nghịch biến trên khoảng (−2; 1).

Hàm số đạt cực đại tại x = −2 và đạt cực tiểu tại x = 1.

a) Đặt f(x) = tanx – x với mọi x ∈ \(\left( {0;\frac{\pi }{2}} \right)\).

Ta có: f'(x) = \(\frac{1}{{{{\cos }^2}x}} - 1\) > 0 với mọi x ∈ \(\left( {0;\frac{\pi }{2}} \right)\).

Do đó f(x) đồng biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\), nên f(x) ≥ f(0) – 0 hay tanx ≥ x với mọi

x ∈ \(\left( {0;\frac{\pi }{2}} \right)\).

b) Đặt f(x) = lnx – x + 1 với mọi x > 0.

Ta có: f'(x) = \(\frac{1}{x}\) − 1

           f'(x) = 0 ⇔ x = 1.

Hàm số đồng biến trên khoảng (0; 1) và nghịch biến trên khoảng (1; +∞).

Do đó f(x) ≤ f(1) – 0 với mọi x > 0  hay lnx ≤ x – 1 với mọi x > 0.

a) Đặt f(x) = x³ + 5x² – 8x + 4

Khi đó, f'(x) = 3x² + 10x – 8.

             f'(x) = 0 ⇔ x = \(\frac{2}{3}\) hoặc x = −4.

Ta có bảng biến thiên như sau:

Từ bảng biến thiên, ta thấy đường thẳng y = 0 giao với đồ thị của hàm số tại đúng một thời điểm trong khoảng (−∞; −4).

Do đó, phương trình x³ + 5x² – 8x + 4 = 0 có duy nhất một nghiệm.

b) Đặt f(x) = −x³ + 3x² + 24x + 1

Ta có: f'(x) = −3x² + 6x + 24

           f'(x) = 0 ⇔ x = −2 hoặc x = 4.

Ta có bảng biến thiên như sau:

Từ bảng biến thiên, ta thấy đường thẳng y = 0 giao với đồ thị của hàm số tại ba điểm phân biệt.

Do đó, phương trình −x³ + 3x² + 24x – 1 = 0 có ba nghiệm phân biệt.