Câu hỏi:
19/09/2024 1,719
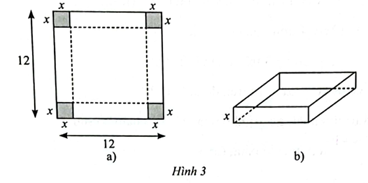
Nam dùng một tấm bìa có kích thước 50 cm x 20 cm để làm một chiếc lon hình trụ (không có nắp).
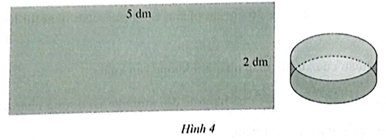
Hỏi cần chọn bán kính đáy hình trụ là bao nhiêu xăngtimét thì lon hình trụ đạt thể tích lớn nhất?
Lưu ý: Kết quả làm tròn đến hàng phần trăm của xăngtimét, bỏ qua phần hao hụt khi cắt và tạo hình, đáy và mặt bên phải là các bìa nguyên vẹn (không ghép nối).
Nam dùng một tấm bìa có kích thước 50 cm x 20 cm để làm một chiếc lon hình trụ (không có nắp).
Hỏi cần chọn bán kính đáy hình trụ là bao nhiêu xăngtimét thì lon hình trụ đạt thể tích lớn nhất?
Lưu ý: Kết quả làm tròn đến hàng phần trăm của xăngtimét, bỏ qua phần hao hụt khi cắt và tạo hình, đáy và mặt bên phải là các bìa nguyên vẹn (không ghép nối).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x (dm) là bán kính đáy hình trụ (x > 0).
Phương án 1:
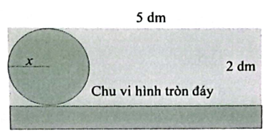
Thể tích lon hình trụ cho bởi công thức:
V(x) = πx2(2 – 2x) với x ∈ \(\left( {0;\frac{5}{{2\pi }}} \right]\).
Khảo sát và vẽ đồ thị hàm số:
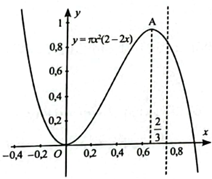
V(x) đạt giá trị lớn nhất trên \(\left( {0;\frac{5}{{2\pi }}} \right]\) là khoảng 0,93 dm3 khi x ≈ 0,67 dm.
Phương án 2:
Thể tích lon hình trụ cho bởi công thức:
V(x) = 2πx2 với x ∈ \(\left( {0;\frac{5}{{2\left( {\pi + 1} \right)}}} \right]\).
Khảo sát và vẽ đồ thị hàm số:
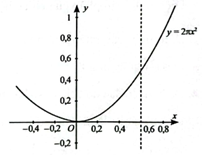
V(x) đạt giá trị lớn nhất trên \(\left( {0;\frac{5}{{2\left( {\pi + 1} \right)}}} \right]\) là khoảng 2,29 dm3 khi x ≈0,60 dm.
Vậy thể tích lon hình trụ lớn nhất khi thiết kế theo phương án 2 và bán kính đáy khoảng 0,60dm.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lợi nhuận xưởng thu được trong một ngày khi sản xuất x (kg) thành phẩm là:
P(x) = 513x – (2x3 – 30x2 + 177x + 2 592) = −2x3 + 30x2 + 336x – 2 592 với 0 ≤ x ≤ 20.
Ta có: P'(x) = −6x2 + 60x + 336
P'(x) = 0 ⇔ x = 14 hoặc x = −4 (loại do −4 ∉ [0; 20]).
Ta có bảng biến thiên:
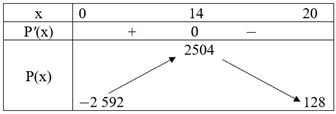
Do đó \(\mathop {\max }\limits_{\left[ {0;20} \right]} P\left( x \right) = P\left( {14} \right) = 2504\).
Vậy x = 14 kg.
Lời giải
Ta có: h(t) = \( - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\) với 0 ≤ t ≤ 20.
h'(t) = \( - \frac{{12}}{{255}}{t^2} + \frac{{98}}{{85}}{t^2} - \frac{{98}}{{17}}\)
h'(t) = 0 ⇔ x = 7 hoặc x = \(\frac{{37}}{5}\).
Bảng xét dấu:
Do đó, tàu lượn đi xuống khi t trong các khoảng (0; 7) và \(\left( {\frac{{37}}{5};20} \right)\), tàu lượn đi lên khi t trong khoảng \(\left( {7;\frac{{37}}{5}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận