Câu hỏi:
19/09/2024 1,081
Cho hàm số y = \(\frac{{2x - 1}}{{ - x + 3}}\). Chứng tỏ rằng đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.
Cho hàm số y = \(\frac{{2x - 1}}{{ - x + 3}}\). Chứng tỏ rằng đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cách 1:
Xét phương trình hoành độ giao điểm, có: \(\frac{{2x - 1}}{{ - x + 3}}\) = −x (x ≠ 3).
⇔ 2x – 1 = −x(−x + 3)
⇔ 2x – 1 = x2 – 3x
⇔ x2 – 5x + 1 = 0
⇔ \(\left\{ \begin{array}{l}{3^2} - 5.3 + 1 = - 5 \ne 0\\\Delta = {( - 5)^2} - 4.1 = 21 > 0\end{array} \right.\)
Vậy phương trình có hai nghiệm phân biệt khác 3.
Vậy đường thẳng y = −x cắt đồ thị hàm số đã cho tại hai điểm phân biệt.
Cách 2:
Ta vẽ được đồ thị hàm số y = \(\frac{{2x - 1}}{{ - x + 3}}\) và đường thẳng y = −x trên cùng một hệ trục Oxy.
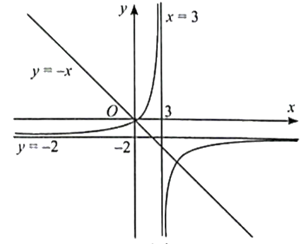
Ta thấy đường thẳng y = −x cắt đồ thị hàm số y = \(\frac{{2x - 1}}{{ - x + 3}}\) tại hai điểm phân biệt.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lợi nhuận xưởng thu được trong một ngày khi sản xuất x (kg) thành phẩm là:
P(x) = 513x – (2x3 – 30x2 + 177x + 2 592) = −2x3 + 30x2 + 336x – 2 592 với 0 ≤ x ≤ 20.
Ta có: P'(x) = −6x2 + 60x + 336
P'(x) = 0 ⇔ x = 14 hoặc x = −4 (loại do −4 ∉ [0; 20]).
Ta có bảng biến thiên:
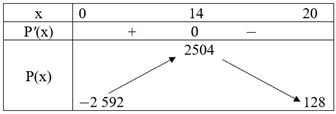
Do đó \(\mathop {\max }\limits_{\left[ {0;20} \right]} P\left( x \right) = P\left( {14} \right) = 2504\).
Vậy x = 14 kg.
Lời giải
Ta có: h(t) = \( - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\) với 0 ≤ t ≤ 20.
h'(t) = \( - \frac{{12}}{{255}}{t^2} + \frac{{98}}{{85}}{t^2} - \frac{{98}}{{17}}\)
h'(t) = 0 ⇔ x = 7 hoặc x = \(\frac{{37}}{5}\).
Bảng xét dấu:
Do đó, tàu lượn đi xuống khi t trong các khoảng (0; 7) và \(\left( {\frac{{37}}{5};20} \right)\), tàu lượn đi lên khi t trong khoảng \(\left( {7;\frac{{37}}{5}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận