Câu hỏi:
19/09/2024 5,110
Người ta muốn thiết kế một quả địa cầu trong không gian Oxyz bằng phần mềm 3D. Biết phương trình mặt cầu là:
(S): (x – 24)2 + (y – 24)2 + (z – 24)2 = 100 (đơn vị cm) và phương trình đường thẳng trục xoay là d: \[\frac{{x - 24}}{1} = \frac{{y - 24}}{1} = \frac{{z - 24}}{{3,25}}\].
a) Tìm tọa độ giao điểm của d và (S).
b) Tính số đo góc giữa d và trục Oz. Làm tròn kết quả đến hàng phần mười của độ.
Người ta muốn thiết kế một quả địa cầu trong không gian Oxyz bằng phần mềm 3D. Biết phương trình mặt cầu là:
(S): (x – 24)2 + (y – 24)2 + (z – 24)2 = 100 (đơn vị cm) và phương trình đường thẳng trục xoay là d: \[\frac{{x - 24}}{1} = \frac{{y - 24}}{1} = \frac{{z - 24}}{{3,25}}\].
a) Tìm tọa độ giao điểm của d và (S).
b) Tính số đo góc giữa d và trục Oz. Làm tròn kết quả đến hàng phần mười của độ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có phương trình tham số của đường thẳng d là: \[\left\{ \begin{array}{l}x = 24 + t\\y = 24 + t\\z = 24 + 3,25t.\end{array} \right.\]
Xét điểm M(24 + t; 24 + t; 24 + 3,25t) thuộc đường thẳng d.
Thay tọa độ của M vào phương trình mặt cầu (S), ta được:
(24 + t – 24)2 + (24 + t – 24)2 + (24 + 3,25t – 24)2 = 100 ⇔ t = \[ \pm \frac{{40\sqrt {201} }}{{201}}\].
Vậy d cắt (S) tại hai điểm \[M\left( {24 + \frac{{40\sqrt {201} }}{{201}};24 + \frac{{40\sqrt {201} }}{{201}};24 + \frac{{130\sqrt {201} }}{{201}}} \right)\] hoặc
\[M'\left( {24 - \frac{{40\sqrt {201} }}{{201}};24 - \frac{{40\sqrt {201} }}{{201}};24 - \frac{{130\sqrt {201} }}{{201}}} \right)\].
b) Vectơ chỉ phương của d và trục Oz lần lượt là \[\overrightarrow a = \left( {1;1;3,25} \right),\overrightarrow k = \left( {0;0;1} \right)\].
Ta có: cos(d; Oz) = \[\frac{{\left| {\overrightarrow a .\overrightarrow k } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow k } \right|}} = \frac{{\left| {3,25} \right|}}{{\sqrt {{1^2} + {1^2} + 3,{{25}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} \approx 0,917\].
Suy ra (d, Oz) ≈ 23,5°.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Gọi (S) là mặt cầu biểu diễn ranh giới của vùng phủ sáng của đèn trên hải đẳng trong không gian Oxyz.
Mặt cầu (S) có tâm I(20; 40; 60) và bán kính R = 3000, suy ra (S) có phương trình:
(x – 20)2 + (y – 40)2 + (z – 60)2 = 9 000 000.
b) Ta có: IM = \[\sqrt {{{400}^2} + {{300}^2} + {{\left( { - 60} \right)}^2}} = 20\sqrt {634} \] ≈ 504 < 3000, suy ra IM < R.
Do đó, người này có thể nhìn thấy được ánh sáng của đèn trên hải đăng.
Lời giải
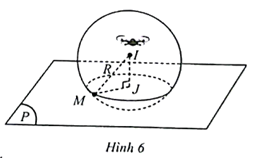
a) Ta có mặt cầu (S): (x – 20)2 + (y – 30)2 + (z – 10)2 = 400 có tâm I(20; 30; 10) và bán kính R = 20 m.
Ta có: IJ = d(I, (P)) = 10 m.
b) Ta có điểm M thuộc mặt cầu (S) nên IM = R = 20 m. Trong tam giác IJM vuông tại J, ta có: JM = \[\sqrt {I{M^2} - {\rm{I}}{{\rm{J}}^2}} = \sqrt {{{20}^2} - {{10}^2}} = 10\sqrt 3 \approx 17,32\] (m).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo