III. Vận dụng
Cho hàm số \(y = \frac{{x + m}}{{x - 2}}\) thỏa mãn \(\mathop {\min }\limits_{\left[ {3;5} \right]} y = 4\). Mệnh đề nào dưới đây đúng
A.\(m > 5\).
B.\(4 \le m \le 5\).
C.\(2 \le m < 4\).
D.\(m < 2\).
Quảng cáo
Trả lời:
Đáp án đúng là: A
Hàm số \(y = \frac{{x + m}}{{x - 2}}\) xác định và liên tục trên \(\left[ {3;5} \right]\). Ta có \(y' = \frac{{ - 2 - m}}{{{{\left( {x - 2} \right)}^2}}}\).
+ Xét \( - 2 - m > 0 \Leftrightarrow m < - 2\,\,\left( * \right)\).
Khi đó hàm số đồng biến trên \(\left[ {3;5} \right]\).
Suy ra \(\mathop {\min }\limits_{\left[ {3;5} \right]} y = y\left( 3 \right) = 3 + m\). Do đó \(3 + m = 4 \Leftrightarrow m = 1\)( không thỏa \(\left( * \right)\)).
+ Xét \( - 2 - m < 0 \Leftrightarrow m > - 2\,\,\,\left( {**} \right)\).</>
Khi đó hàm số nghịch biến trện \(\left[ {3;5} \right]\).
Suy ra \(\mathop {\min }\limits_{\left[ {3;5} \right]} y = y\left( 5 \right) = \frac{{5 + m}}{3}\). Do đó \(\frac{{5 + m}}{3} = 4 \Leftrightarrow m = 7\)( thỏa \(\left( {**} \right)\)).
Vậy \(m = 7 > 5\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 243 m/s.
B. 27 m/s.
C. 144 m/s.
D. 36 m/s.
Lời giải
Đáp án đúng là: D
Ta có v = s' = −t2 + 12t; v' = −2t + 12; v' = 0 t = 6.
Bảng biến thiên
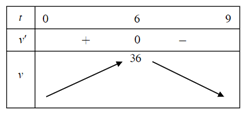
Từ bảng biến thiên, ta thấy vận tốc lớn nhất của vật là 36 m/s.
Lời giải
Đáp án đúng là: A
Vận tốc của chuyển động là v(t) = s' = 12t – 3t2, t > 0.
Có v'(t) = −6t + 12; v'(t) = 0 t = 2.
Bảng biến thiên
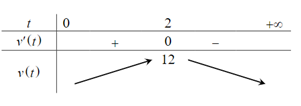
Dựa vào bảng biến thiên ta thấy vận tốc v(m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm t = 2.
Câu 3
A. \(M + m = 7\).
B. \(M + m = \frac{{16}}{3}\) .
C. \(M + m = \frac{{13}}{3}\).
D. \(M + m = 5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(2 + \sqrt 3 \).
B. \(2\).
C. 0.
D. \(\sqrt 3 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Không tồn tại.
B. \(0\).
C. \(2.\)
D. \( - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(f\left( { - 1} \right)\).
B. \(f\left( 3 \right)\).
C. \(f\left( 2 \right)\).
D. \(f\left( 0 \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số y = f ( x ) liên tục trên đoạn [ − 1 ; 3 ] và có bảng biến thiên như sau Giá trị lớn nhất của hàm số y = f ( x ) trên đoạn [ − 1 ; 3 ] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040661.png)
![Cho hàm số f ( x ) liên tục trên [ − 1 ; 5 ] và có đồ thị như sau Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) trên đoạn [ − 1 ; 5 ] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040859.png)