Câu hỏi:
25/10/2024 51
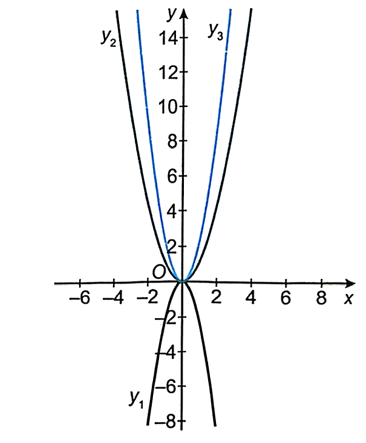
Cho hàm số y = f(x) = ax2 (a ≠ 0).
a) Chứng tỏ rằng nếu (x0; y0) là một điểm thuộc đồ thị hàm số thì điểm (–x0; y0) cũng nằm trên đồ thị hàm số đó.
b) Chứng minh rằng f(–x) = f(x) với mọi x thuộc ℝ.
Cho hàm số y = f(x) = ax2 (a ≠ 0).
a) Chứng tỏ rằng nếu (x0; y0) là một điểm thuộc đồ thị hàm số thì điểm (–x0; y0) cũng nằm trên đồ thị hàm số đó.
b) Chứng minh rằng f(–x) = f(x) với mọi x thuộc ℝ.
Câu hỏi trong đề:
Giải SBT Toán 9 KNTT Bài 18. Hàm số y = ax2 (a ≠ 0) có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Giả sử (x0; y0) là một điểm thuộc đồ thị hàm số y = f(x) = ax2 (a ≠ 0).
Khi đó ta có: y0 = ax02.
Mà y0 = ax02 = a(–x0)2 nên điểm (–x0; y0) cũng nằm trên đồ thị hàm số đó.
b) Với mọi x thuộc ℝ, ta có:
F(–x) = a(–x)2 = ax2 = f(x).
Do đó f(–x) = f(x) với mọi x thuộc ℝ. (đpcm)
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong hình bên có đồ thị của ba hàm số y = –2x2, y = x2, y = 2x2.
a) Cho biết đường nào là đồ thị của hàm số y = –2x2.
b) Trong hai đường còn lại, với mỗi x hãy so sánh hai giá trị tương ứng của y để phân biệt đồ thị hai hàm số y = x2 và y = 2x2.
Trong hình bên có đồ thị của ba hàm số y = –2x2, y = x2, y = 2x2.
a) Cho biết đường nào là đồ thị của hàm số y = –2x2.
b) Trong hai đường còn lại, với mỗi x hãy so sánh hai giá trị tương ứng của y để phân biệt đồ thị hai hàm số y = x2 và y = 2x2.
Xem đáp án »
25/10/2024
107
Câu 2:
Thể tích V của hình lăng trụ đứng tứ giác có đáy là hình vuông và chiều cao 5 cm là một hàm số của độ dài cạnh đáy a (cm).
a) Viết công thức của hàm số này và tính độ dài cạnh đáy của hình lăng trụ nếu biết thể tích bằng 180 cm3.
b) Nếu độ dài cạnh a của hình vuông đáy tăng lên hai lần thì thể tích V của khối lăng trụ thay đổi như thế nào?
Thể tích V của hình lăng trụ đứng tứ giác có đáy là hình vuông và chiều cao 5 cm là một hàm số của độ dài cạnh đáy a (cm).
a) Viết công thức của hàm số này và tính độ dài cạnh đáy của hình lăng trụ nếu biết thể tích bằng 180 cm3.
b) Nếu độ dài cạnh a của hình vuông đáy tăng lên hai lần thì thể tích V của khối lăng trụ thay đổi như thế nào?
Xem đáp án »
19/10/2024
103
Câu 3:
Xác định hệ số a của hàm số y = ax2 (a ≠ 0), biết đồ thị của hàm số đi qua điểm:
a) ;
b) .
Xác định hệ số a của hàm số y = ax2 (a ≠ 0), biết đồ thị của hàm số đi qua điểm:
a) ;
b) .
Xem đáp án »
25/10/2024
54
Câu 4:
Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng toạ độ: y = 0,75x2; y = –0,75x2.
Có nhận xét gì về vị trí của hai đồ thị này so với trục hoành Ox?
Vẽ đồ thị của hai hàm số sau trên cùng một mặt phẳng toạ độ: y = 0,75x2; y = –0,75x2.
Có nhận xét gì về vị trí của hai đồ thị này so với trục hoành Ox?
Xem đáp án »
25/10/2024
48
Câu 5:
Cầu treo Sunshine Skyway bắc qua Vịnh Tampa ở bang Florida (Mỹ), được hỗ trợ bởi 21 dây cáp làm bằng thép, mỗi dây có đường kính 9 inch. Khối lượng mà mỗi dây cáp có thể chịu được là w = 8d2 (tấn), trong đó d là đường kính của dây cáp (tính bằng inch) (Theo Algebra 2, NXB McGraw–Hill, 2018).
a) Tính khối lượng tối đa mà cây cầu treo có thể chịu đựng được.
b) Nếu muốn cây cầu treo có thể chịu được khối lượng là 15 162 tấn thì đường kính của dây cáp phải là bao nhiêu?
Cầu treo Sunshine Skyway bắc qua Vịnh Tampa ở bang Florida (Mỹ), được hỗ trợ bởi 21 dây cáp làm bằng thép, mỗi dây có đường kính 9 inch. Khối lượng mà mỗi dây cáp có thể chịu được là w = 8d2 (tấn), trong đó d là đường kính của dây cáp (tính bằng inch) (Theo Algebra 2, NXB McGraw–Hill, 2018).
a) Tính khối lượng tối đa mà cây cầu treo có thể chịu đựng được.
b) Nếu muốn cây cầu treo có thể chịu được khối lượng là 15 162 tấn thì đường kính của dây cáp phải là bao nhiêu?
Xem đáp án »
19/10/2024
44
Câu 6:
Trên cùng một mặt phẳng toạ độ Oxy, vẽ và đường thẳng (d): y = x – 2. Dùng đồ thị xác định toạ độ các giao điểm của hai đường này.
Trên cùng một mặt phẳng toạ độ Oxy, vẽ và đường thẳng (d): y = x – 2. Dùng đồ thị xác định toạ độ các giao điểm của hai đường này.
Xem đáp án »
25/10/2024
44
về câu hỏi!