Câu hỏi:
26/12/2024 6,211
Cô Liên gửi \[100\] triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là \[12\] tháng với lãi suất \(6\% \) một năm. Giả sử qua các năm thì lãi suất không thay đổi và cô Liên không gửi thêm tiền vào mỗi năm. Hỏi sau ít nhất bao nhiêu năm thì số tiền cô Liên có được cả gốc và lãi nhiều hơn \[150\] triệu đồng (làm tròn kết quả đến hàng đơn vị)?
Cô Liên gửi \[100\] triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là \[12\] tháng với lãi suất \(6\% \) một năm. Giả sử qua các năm thì lãi suất không thay đổi và cô Liên không gửi thêm tiền vào mỗi năm. Hỏi sau ít nhất bao nhiêu năm thì số tiền cô Liên có được cả gốc và lãi nhiều hơn \[150\] triệu đồng (làm tròn kết quả đến hàng đơn vị)?
Câu hỏi trong đề: 43 bài tập Phương trình và bất phương trình có lời giải !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Số tiền sau \(t\) năm mà cô Liên có là: \(S = 100 \cdot {\left( {1,06} \right)^t}\).
Xét bất phương trình: \(100 \cdot {\left( {1,06} \right)^t} > 150 \Leftrightarrow {\left( {1,06} \right)^t} > \frac{{150}}{{100}} \Leftrightarrow t > {\log _{1,06}}\left( {1,5} \right)\).
Vì \({\log _{1,06}}\left( {1,5} \right) \approx 6,96\) nên \(t > 6,96\).
Vậy sau ít nhất \(7\) năm thì số tiền cô Liên có được cả gốc và lãi nhiều hơn \[150\] triệu đồng.
Đáp án: \(7\).
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho phương trình \({\log _3}\left( {x + 6} \right) = {\log _3}\left( {x - 1} \right) + 1\) (*).
a) Điều kiện xác định của phương trình: \(x > 1\).
b) Phương trình (*) có chung tập nghiệm với phương trình \(\frac{{{x^2} - 11x + 9}}{{x - 1}} = 0\).
c) Gọi \(x = a\) là nghiệm của phương trình (*), khi đó \(\mathop {\lim }\limits_{x \to a} \left( {x - 3} \right) = \frac{5}{2}\).
d) Nghiệm của phương trình (*) là hoành độ giao điểm của đường thẳng \({d_1}:2x - y - 8 = 0\) với đường thẳng \({d_2}:y = 0\).
Xem đáp án »
26/12/2024
9,276
Câu 2:
Một cây cầu có dạng cung \(AB\) của đồ thị hàm số \(y = 4,8\cos \frac{x}{9}\) và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở hình vẽ dưới đây.
Một sà lan chở khối hàng hoá được xếp thành hình hộp chữ nhật với độ cao \(3,6\,{\rm{m}}\) so với mực nước sông. Hỏi chiều rộng của khối hàng hoá đó lớn nhất là bao nhiêu mét để sà lan có thể đi qua được gầm cầu (làm tròn kết quả đến hàng đơn vị)?
Một cây cầu có dạng cung \(AB\) của đồ thị hàm số \(y = 4,8\cos \frac{x}{9}\) và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở hình vẽ dưới đây.
Một sà lan chở khối hàng hoá được xếp thành hình hộp chữ nhật với độ cao \(3,6\,{\rm{m}}\) so với mực nước sông. Hỏi chiều rộng của khối hàng hoá đó lớn nhất là bao nhiêu mét để sà lan có thể đi qua được gầm cầu (làm tròn kết quả đến hàng đơn vị)?
Xem đáp án »
26/12/2024
3,634
Câu 3:
Cho phương trình \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
a) Hạ bậc hai vế, ta được phương trình \(\frac{{1 + \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 - \cos \left( {2x + \pi } \right)}}{2}\).
b) Ta có \(\cos \left( {2x + \pi } \right) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = & \frac{\pi }{{12}} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
Cho phương trình \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
a) Hạ bậc hai vế, ta được phương trình \(\frac{{1 + \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 - \cos \left( {2x + \pi } \right)}}{2}\).
b) Ta có \(\cos \left( {2x + \pi } \right) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = & \frac{\pi }{{12}} + k\frac{\pi }{3}\,\,\left( {k \in \mathbb{Z}} \right)\).
Xem đáp án »
26/12/2024
3,343
Câu 4:
Cho hai đồ thị hàm số \(y = \sin \left( {x + \frac{\pi }{4}} \right)\) và \(y = \sin x\).
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: \(\sin \left( {x + \frac{\pi }{4}} \right) = \sin x\).
b) Hoành độ giao điểm của hai đồ thị là \(x = \frac{{3\pi }}{8} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
c) Khi \[x \in \left[ {0;2\pi } \right]\] thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi \(x \in \left[ {0;2\pi } \right]\) thì toạ độ giao điểm của hai đồ thị hàm số là: \(\left( {\frac{{5\pi }}{8};\sin \frac{{5\pi }}{8}} \right),\left( {\frac{{7\pi }}{8};\sin \frac{{7\pi }}{8}} \right)\).
Cho hai đồ thị hàm số \(y = \sin \left( {x + \frac{\pi }{4}} \right)\) và \(y = \sin x\).
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số: \(\sin \left( {x + \frac{\pi }{4}} \right) = \sin x\).
b) Hoành độ giao điểm của hai đồ thị là \(x = \frac{{3\pi }}{8} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
c) Khi \[x \in \left[ {0;2\pi } \right]\] thì hai đồ thị hàm số cắt nhau tại ba điểm.
d) Khi \(x \in \left[ {0;2\pi } \right]\) thì toạ độ giao điểm của hai đồ thị hàm số là: \(\left( {\frac{{5\pi }}{8};\sin \frac{{5\pi }}{8}} \right),\left( {\frac{{7\pi }}{8};\sin \frac{{7\pi }}{8}} \right)\).
Xem đáp án »
26/12/2024
2,115
Câu 6:
Một vật dao động xung quanh vị trí cân bằng theo phương trình \(x = 1,5\cos \left( {\frac{{t\pi }}{4}} \right)\); trong đó \(t\) là thời gian được tính bằng giây và quãng đường \(h = \left| x \right|\) được tính bằng mét là khoảng cách theo phương ngang của chất điểm đối với vị trí cân bằng (xem hình bên).
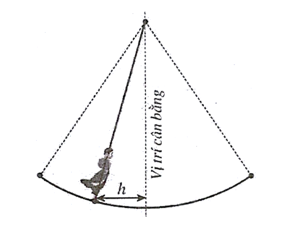
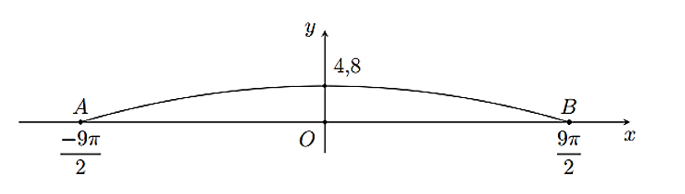
a) Vật ở xa vị trí cân bằng nhất nghĩa là \(h = 1,5\;\,{\rm{m}}\).
b) Trong 10 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì \(\cos \left( {\frac{{t\pi }}{4}} \right) = 0\).
d) Trong khoảng từ 0 đến 20 giây thì vật đi qua vị trí cân bằng 4 lần.
Xem đáp án »
26/12/2024
1,740
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
50 bài tập Nguyên hàm, tích phân và ứng dụng có lời giải
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận