Người ta dùng một thanh thép có chiều dài 4 m để uốn thành khung viền của một cửa sổ có dạng một hình chữ nhật ghép với nửa hình tròn có các kích thước được cho như hình bên.
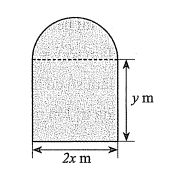
a) Có thể biểu thị \(y\) theo công thức \(y = 2 - \frac{{\left( {\pi - 2} \right)x}}{2}\).
b) Diện tích của cửa sổ được tính bởi công thức \(S\left( x \right) = 4x - 2{x^2} - \frac{{\pi {x^2}}}{2}\) (m2).
c) Diện tích của cửa sổ lớn nhất khi \(x = \frac{4}{{\pi + 2}}\) (m).
d) Giá trị lớn nhất của diện tích cửa sổ là \(\frac{8}{{\pi + 4}}\) (m2).
Người ta dùng một thanh thép có chiều dài 4 m để uốn thành khung viền của một cửa sổ có dạng một hình chữ nhật ghép với nửa hình tròn có các kích thước được cho như hình bên.

a) Có thể biểu thị \(y\) theo công thức \(y = 2 - \frac{{\left( {\pi - 2} \right)x}}{2}\).
b) Diện tích của cửa sổ được tính bởi công thức \(S\left( x \right) = 4x - 2{x^2} - \frac{{\pi {x^2}}}{2}\) (m2).
c) Diện tích của cửa sổ lớn nhất khi \(x = \frac{4}{{\pi + 2}}\) (m).
d) Giá trị lớn nhất của diện tích cửa sổ là \(\frac{8}{{\pi + 4}}\) (m2).
Câu hỏi trong đề: 44 bài tập Đạo hàm và khảo sát hàm số có lời giải !!
Quảng cáo
Trả lời:
Ta có \(2x + 2y + \pi x = 4\), suy ra \(y = 2 - \frac{{\left( {\pi + 2} \right)x}}{2}\).
\(S\left( x \right) = 2xy + \frac{{\pi {x^2}}}{2} = 2x\left( {2 - x - \frac{{\pi x}}{2}} \right) + \frac{{\pi {x^2}}}{2} = 4x - 2{x^2} - \frac{{\pi {x^2}}}{2}\) (m2).
Ta có \(x > 0\) và \(y > 0\), suy ra \(0 < x < \frac{4}{{\pi + 2}}\).
\(S'\left( x \right) = 4 - 4x - \pi x;\,\,S'\left( x \right) = 0 \Leftrightarrow x = \frac{4}{{\pi + 4}}\).
Bảng biến thiên
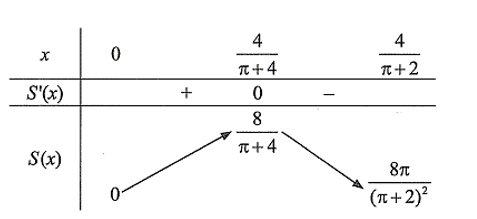
Vậy diện tích của cửa sổ lớn nhất khi \(x = \frac{4}{{\pi + 4}}\) (m). Giá trị lớn nhất là \(\frac{8}{{\pi + 4}}\) (m2).
Đáp án: a) Sai, b) Đúng, c) Sai, d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số máy móc công ty sử dụng để sản xuất là \(x\,\,\left( {x \in \mathbb{N},\,\,x > 0} \right)\).
Thời gian cần để sản xuất hết \(8000\) quả bóng là: \(\frac{{8000}}{{30x}}\) (giờ).
Tổng chi phí để sản xuất là: \(P\left( x \right) = 200x + \frac{{8000}}{{30x}} \cdot 192 = 200x + \frac{{51200}}{x}\).
Ta có: \(P'\left( x \right) = 200 - \frac{{51200}}{{{x^2}}} = 0 \Leftrightarrow {x^2} = 256 \Leftrightarrow \left[ \begin{array}{l}x = 16\\x = - 16\left( L \right)\end{array} \right.\).
Bảng biến thiên:
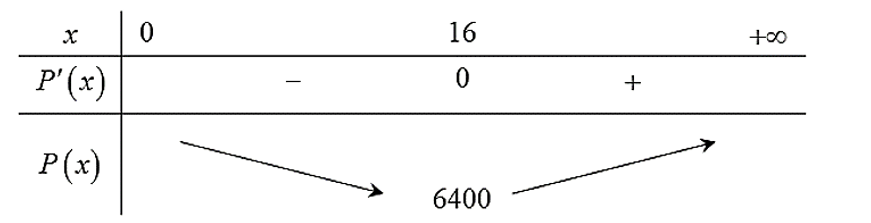
Vậy công ty nên sử dụng \(16\) máy để chi phí hoạt động là thấp nhất.
Đáp án: \(16.\)
Lời giải
Ta có \(f'\left( x \right) = {\left( {x - \sin 2x} \right)^\prime } = 1 - 2\cos 2x\).
\(f'\left( x \right) = 0 \Leftrightarrow 1 - 2\cos 2x = 0 \Leftrightarrow \cos 2x = \frac{1}{2}\)\[ \Leftrightarrow 2x = \pm \frac{\pi }{3} + 2k\pi \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\].
Với \(x \in \left[ {0;\pi } \right]\) thì phương trình\(f'\left( x \right) = 0\) có nghiệm\[x = \frac{\pi }{6}\] hoặc \[x = \frac{{5\pi }}{6}\].
Có \(f\left( 0 \right) = 0\); \(f\left( {\frac{\pi }{6}} \right) = \frac{\pi }{6} - \frac{{\sqrt 3 }}{2};\,\,f\left( {\frac{{5\pi }}{6}} \right) = \frac{{5\pi }}{6} + \frac{{\sqrt 3 }}{2};\,\,f\left( \pi \right) = \pi \).
Vậy giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{{5\pi }}{6} + \frac{{\sqrt 3 }}{2}\).
Đáp án: a) Sai, b) Sai, c) Sai, d) Đúng.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\] và \[\left( {1; + \infty } \right)\].
B. Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]\[ \cup \]\[\left( {1; + \infty } \right)\].
C. Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\] và \[\left( {1; + \infty } \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.