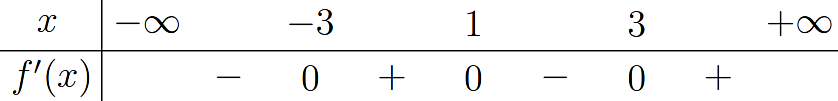Cho hàm số y = f(x) có đạo hàm f'(x) = (1 - x)2(x + 1)3(3 – x), ∀x ∈ ℝ. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. (−∞; 1);
B. (−∞; −1);
C. (−1; 3);
D. (3; +∞).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Ta có: f'(x) = 0 (1 - x)2(x + 1)3(3 – x) = 0 x = 1 hoặc x = −1 hoặc x = 3.
Bảng xét dấu:
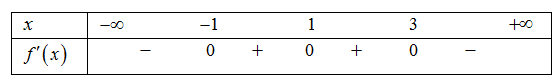
Từ bảng xét dấu ta thấy hàm số đồng biến trên khoảng (−1; 3).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 5;
B. 3;
C. 2;
D. 4.
Lời giải
Đáp án đúng là: C
Ta có f'(x) = (x – 1)2(x2 – 5x + 6) = (x – 1)2(x −2)(x − 3).
Do f'(x) = 0 có 1 nghiệm kép x = 1 và hai nghiệm đơn x = 2, x = 3 nên f'(x) đổi dấu hai lần khi qua x = 2 và x = 3. Do đó hàm số có 2 điểm cực trị.
Câu 2
A. 0;
B. 1;
C. 2;
D. 3.
Lời giải
Đáp án đúng là: B
Ta có f'(x) = 0 x = 1, suy ra f'(x) đổi dấu một lần khi x đi qua giá trị x = 1 nên hàm số f(x) có 1 điểm cực trị.
Câu 3
A. 3;
B. 4;
C. 2;
D. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hàm số có 4 điểm cực trị;
B. Hàm số có 2 điểm cực đại;
C. Hàm số có 1 điểm cực trị;
D. Hàm số có 2 điểm cực tiểu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 1;
B. 2;
C. 3;
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo