Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình dưới đây. Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = - 1,x = 4\). Khi đó:
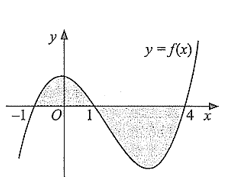
a) Diện tích \(S\) của hình phẳng \(\left( H \right)\) là \(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} \).
b) Diện tích \(S\) của hình phẳng \(\left( H \right)\) là \(S = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^4 {f\left( x \right){\rm{d}}x} \).
c) Nếu \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) thì \(F\left( 1 \right) > F\left( { - 1} \right) > F\left( 4 \right)\).
d) Thể tích vật thể được tạo thành khi quay \(\left( H \right)\) quanh trục hoành là \(V = \int\limits_{ - 1}^4 {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} \).
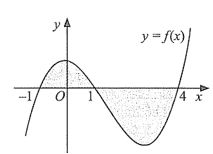
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình dưới đây. Gọi \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = - 1,x = 4\). Khi đó:

a) Diện tích \(S\) của hình phẳng \(\left( H \right)\) là \(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} \).
b) Diện tích \(S\) của hình phẳng \(\left( H \right)\) là \(S = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^4 {f\left( x \right){\rm{d}}x} \).
c) Nếu \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)\) thì \(F\left( 1 \right) > F\left( { - 1} \right) > F\left( 4 \right)\).
d) Thể tích vật thể được tạo thành khi quay \(\left( H \right)\) quanh trục hoành là \(V = \int\limits_{ - 1}^4 {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} \).
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Ta có \(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} \). Từ đồ thị, ta có:
\(S = \int\limits_{ - 1}^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - 1}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} + \int\limits_1^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} \)\( = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} - \int\limits_1^4 {f\left( x \right){\rm{d}}x} \).
Ta có “diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = 1,x = 4\)” lớn hơn “diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và các đường thẳng \(x = - 1,x = 1\)”.
Do đó \(\int\limits_1^4 {\left| {f\left( x \right)} \right|{\rm{d}}x} > \int\limits_{ - 1}^1 {\left| {f\left( x \right)} \right|{\rm{d}}x} \).
Suy ra \(\left| {\left. {F\left( x \right)} \right|_1^4} \right| > \left| {\left. {F\left( x \right)} \right|_{ - 1}^1} \right|\), suy ra \(F\left( 1 \right) - F\left( 4 \right) > F\left( 1 \right) - F\left( { - 1} \right)\)\( \Rightarrow F\left( { - 1} \right) > F\left( 4 \right)\) (1)
Mà \(F\left( x \right)\) đồng biến trên \(\left( { - 1;1} \right)\), nghịch biến trên \(\left( {1;4} \right)\), do đó \(F\left( 1 \right) > F\left( { - 1} \right)\) (2).
Từ (1) và (2) suy ra \(F\left( 1 \right) > F\left( { - 1} \right) > F\left( 4 \right)\).
Ta có \(V = \pi \int\limits_{ - 1}^1 {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} + \pi \int\limits_1^4 {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x = \pi \int\limits_{ - 1}^4 {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} } \).
Đáp án: a) Đúng, b) Sai, c) Đúng, d) Sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(f\left( x \right)\) là lợi nhuận mà lái xe có thể thu về khi chở \(x\) (người) \(\left( {x \in {\mathbb{N}^*}} \right)\) trong chuyến xe đó.
Khi đó: \(f\left( x \right) = \frac{1}{2}x{\left( {40 - x} \right)^2}\), với \(0 < x \le 16\).
Ta có: \(f'\left( x \right) = \frac{1}{2}\left[ {{{\left( {40 - x} \right)}^2} - 2x\left( {40 - x} \right)} \right] = \frac{1}{2}\left( {40 - x} \right)\left( {40 - 3x} \right)\).
Với \(0 < x \le 16\) thì \(f'\left( x \right) = 0 \Leftrightarrow x = \frac{{40}}{3}\).
Mà \(13 < \frac{{40}}{3} < 14\) nên ta có bảng biến thiên như sau:
![Một xe ô tô chở khách du lịch có sức chứa tối đa là \[16\] hành khách. Trong một khu du lịch, một đoàn khách gồm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid18-1737298185.png)
Với \(f\left( {13} \right) = 4738,5,\,\,f\left( {14} \right) = 4732\).
Căn cứ vào bảng biến thiên ta có \[\mathop {\max }\limits_{\left( {0;16} \right]} f\left( x \right) = 4738,5\] (nghìn đồng).
Vậy người lái xe đó có thể thu được nhiều nhất khoảng 4,74 triệu đồng từ một chuyến chở khách.
Đáp án: \(4,74\).
Lời giải
Xét các biến cố: \(A\): “Chọn được bệnh nhân thường xuyên bị stress”;
\(B\): “Chọn được bệnh nhân bị đau dạ dày”.
Khi đó, \(P\left( A \right) = 0,3;P\left( B \right) = 0,4;P\left( {B\mid A} \right) = 0,8\).
Suy ra xác suất chọn được bệnh nhân thường xuyên bị stress vừa bị đau dạ dày là
\(P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( {B\mid A} \right) = 0,3 \cdot 0,8 = 0,24\);
Xác suất chọn được bệnh nhân thường xuyên bị stress, biết bệnh nhân đó bị đau dạ dày, là \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{{0,24}}{{0,4}} = 0,6\).
Đáp án: a) Đúng, b) Đúng, c) Đúng, d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).
C. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AN} = 3\overrightarrow {AG} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.