Câu hỏi:
19/01/2025 140
Lương tháng của 50 nhân viên một công ty được biểu diễn ở biểu đồ sau:
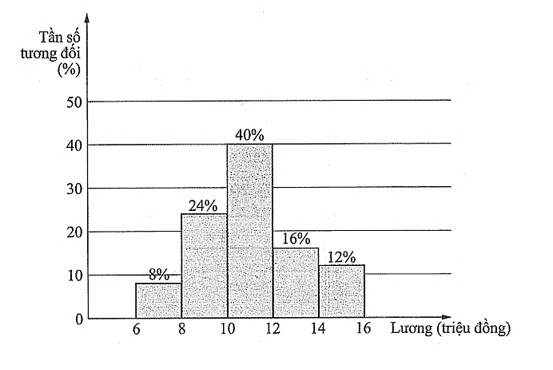
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (đơn vị: triệu đồng, làm tròn kết quả đến hàng phần trăm).
Lương tháng của 50 nhân viên một công ty được biểu diễn ở biểu đồ sau:
Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (đơn vị: triệu đồng, làm tròn kết quả đến hàng phần trăm).
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có bảng tần số ghép nhóm
|
Nhóm |
\(\left[ {6;\,8} \right)\) |
\(\left[ {8;\,10} \right)\) |
\(\left[ {10;\,12} \right)\) |
\(\left[ {12;\,14} \right)\) |
\(\left[ {14;\,16} \right)\) |
|
Tần số |
4 |
12 |
20 |
8 |
6 |
Tứ phân vị thứ nhất \({Q_1} = 8 + \frac{{\frac{{50}}{4} - 4}}{{12}} \cdot \left( {10 - 8} \right) = \frac{{113}}{{12}}\).
Tứ phân vị thứ ba \({Q_3} = 12 + \frac{{\frac{{50 \cdot 3}}{4} - 36}}{8} \cdot \left( {14 - 12} \right) = \frac{{99}}{8}\).
Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{99}}{8} - \frac{{113}}{{12}} = \frac{{71}}{{24}} \approx 2,96\).
Đáp án: \(2,96\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Do \(M\) thuộc mặt phẳng \(\left( P \right)\) và \(MA = MB\) nên \(M\) thuộc giao tuyến của mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( Q \right)\), trong đó \(\left( Q \right)\) là mặt phẳng trung trực của đoạn thẳng \(AB\).
Tọa độ trung điểm của \(AB\) là \(I\left( {2;1; - 1} \right)\) và \(\overrightarrow {AB} = \left( {0; - 2; - 2} \right)\).
Mặt phẳng \(\left( Q \right)\) đi qua \(I\left( {2;1; - 1} \right)\) và có vectơ pháp tuyến \(\overrightarrow {{n_Q}} = \left( {0;1;1} \right)\) có phương trình là
\(\left( {y - 1} \right) + \left( {z + 1} \right) = 0 \Leftrightarrow y + z = 0\).
Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( P \right),\left( Q \right)\).
Gọi \(M\left( {x;y;z} \right) \in d\). Khi đó tọa độ điểm \(M\) là nghiệm của hệ \(\left\{ \begin{array}{l}y + z = 0\\x + 2y - z - 1 = 0\end{array} \right.\).
Đặt \(z = t\). Khi đó ta có \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - t\\z = t\end{array} \right.\).
Suy ra phương trình tham số của \(d:\left\{ \begin{array}{l}x = 1 + 3t\\y = - t\\z = t\end{array} \right.\). Mà \(M \in d\)\( \Rightarrow M\left( {1 + 3t; - t;t} \right)\).
Ta có \(\overrightarrow {AM} = \left( {3t - 1; - t - 2;t} \right),\overrightarrow {BM} = \left( {3t - 1; - t;t + 2} \right)\).
Ta có \(\cos \left( {\overrightarrow {AM} ,\overrightarrow {BM} } \right) = \frac{{{{\left( {3t - 1} \right)}^2} + 2\left( {{t^2} + 2t} \right)}}{{{{\left( {3t - 1} \right)}^2} + {t^2} + {{\left( {t + 2} \right)}^2}}}\)
\( = \frac{{11{t^2} - 2t + 1}}{{11{t^2} - 2t + 5}} = 1 - \frac{4}{{11{t^2} - 2t + 5}} = 1 - \frac{4}{{11{{\left( {t - \frac{1}{{11}}} \right)}^2} + \frac{{54}}{{11}}}}\).
Suy ra \(\widehat {AMB}\) lớn nhất khi và chỉ khi \(t = \frac{1}{{11}}\).
Do đó \(M\left( {\frac{{14}}{{11}}; - \frac{1}{{11}};\frac{1}{{11}}} \right)\)\( \Rightarrow S = a + b + c = \frac{{14}}{{11}} \approx 1,27\).
Đáp án: \(1,27\).
Lời giải
Để dân số nước ta vượt 120 triệu người thì: \[98\,\,564\,\,407 \cdot {{\rm{e}}^{0,0093t}} > 120\,\,000\,\,000\]
\[ \Leftrightarrow t > \frac{1}{{0,0093}}\ln \frac{{120\,\,000\,\,000}}{{98\,\,564\,\,407}} \approx 21,16\]nên \[t > 21,16\].
Vậy kể từ năm 2043 trở đi dân số nước ta vượt 120 triệu người.
Đáp án: \(2043\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 11)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận