Đề thi ôn tốt nghiệp THPT Toán có lời giải ( Đề 3)
28 người thi tuần này 4.6 4.5 K lượt thi 20 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên ĐH KHTN Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Danh sách câu hỏi:
Câu 1
Lời giải
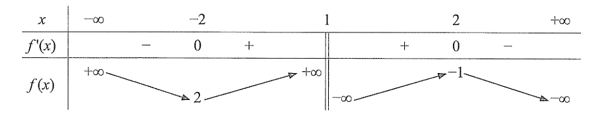
Đồ thị hàm số \(y = f\left( x \right)\) không có điểm chung với đường thẳng \(y = \frac{3}{2}\) nên phương trình \(f\left( x \right) = \frac{3}{2}\) hay \(2f\left( x \right) - 3 = 0\) vô nghiệm. Chọn A.
Câu 2
Lời giải
Đồ thị hàm số đã cho đối xứng nhau qua \(Oy\) nên là hàm số chẵn.
Do đó hàm số đã cho là hàm số \(y = \cos x\). Chọn B.
Câu 3
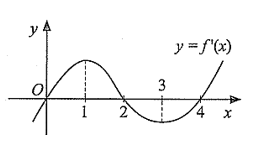
A. Hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\).
B. Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {2;4} \right)\).
C. Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại \(x = 3\).
Lời giải
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\), ta thấy \(f'\left( x \right) < 0\) với \(x \in \left( {2;4} \right)\).
Do đó hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {2;4} \right)\). Chọn B.
Câu 4
A. \(y = 2x\).
B. \(y = - x\).
Lời giải
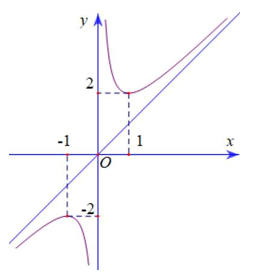
Dựa vào đồ thị hàm số, ta thấy đường tiệm cận xiên của đồ thị hàm số đi qua 2 điểm \(\left( {1;1} \right)\) và \(\left( { - 1; - 1} \right)\) nên đường tiệm cận xiên của đồ thị hàm số có phương trình \(y = x\). Chọn C.
Câu 5
Lời giải
\(\int\limits_{ - 2}^2 {f\left( x \right){\rm{d}}x} = \int\limits_{ - 2}^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^2 {f\left( x \right){\rm{d}}x} \)\( = \int\limits_{ - 2}^1 {\left( {3{x^2} + 2} \right){\rm{d}}x} + \int\limits_1^2 {\left( {8x - 3} \right){\rm{d}}x} \)
\( = \left. {\left( {{x^3} + 2x} \right)} \right|_{ - 2}^1 + \left. {\left( {4{x^2} - 3x} \right)} \right|_1^2\)\( = 15 + 9 = 24\). Chọn B.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.