Một cái hộp hình lập phương, bên trong nó đựng một mô hình đồ chơi có dạng hình chóp tứ giác đều mà đỉnh của hình chóp đó trùng với tâm của một mặt chiếc hộp, giả sử hình vuông đáy của hình chóp trùng với một mặt của chiếc hộp (mặt này cùng với mặt chứa đỉnh hình chóp là hai mặt đối nhau). Biết cạnh của chiếc hộp bằng \(30\;{\rm{cm}}\), hãy tính thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp (mô hình đồ hơi được làm bởi chất liệu nhựa đặc bên trong, kết quả có đơn vị là dm3).
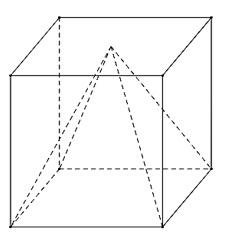
Một cái hộp hình lập phương, bên trong nó đựng một mô hình đồ chơi có dạng hình chóp tứ giác đều mà đỉnh của hình chóp đó trùng với tâm của một mặt chiếc hộp, giả sử hình vuông đáy của hình chóp trùng với một mặt của chiếc hộp (mặt này cùng với mặt chứa đỉnh hình chóp là hai mặt đối nhau). Biết cạnh của chiếc hộp bằng \(30\;{\rm{cm}}\), hãy tính thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp (mô hình đồ hơi được làm bởi chất liệu nhựa đặc bên trong, kết quả có đơn vị là dm3).

Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Đổi \(30\;{\rm{cm}} = 3\;{\rm{dm}}\).
Thể tích hình chóp là \({V_1} = \frac{1}{3} \cdot 3 \cdot {3^2} = 9\) (dm3).
Thể tích khối hộp hình lập phương là \(V = {3^3} = 27\)(dm3).
Thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp là \({V_2} = V - {V_1} = 27 - 9 = 18\)(dm3).
Đáp án: \(18\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Do \(M\) thuộc mặt phẳng \(\left( P \right)\) và \(MA = MB\) nên \(M\) thuộc giao tuyến của mặt phẳng \(\left( P \right)\) và mặt phẳng \(\left( Q \right)\), trong đó \(\left( Q \right)\) là mặt phẳng trung trực của đoạn thẳng \(AB\).
Tọa độ trung điểm của \(AB\) là \(I\left( {2;1; - 1} \right)\) và \(\overrightarrow {AB} = \left( {0; - 2; - 2} \right)\).
Mặt phẳng \(\left( Q \right)\) đi qua \(I\left( {2;1; - 1} \right)\) và có vectơ pháp tuyến \(\overrightarrow {{n_Q}} = \left( {0;1;1} \right)\) có phương trình là
\(\left( {y - 1} \right) + \left( {z + 1} \right) = 0 \Leftrightarrow y + z = 0\).
Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( P \right),\left( Q \right)\).
Gọi \(M\left( {x;y;z} \right) \in d\). Khi đó tọa độ điểm \(M\) là nghiệm của hệ \(\left\{ \begin{array}{l}y + z = 0\\x + 2y - z - 1 = 0\end{array} \right.\).
Đặt \(z = t\). Khi đó ta có \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - t\\z = t\end{array} \right.\).
Suy ra phương trình tham số của \(d:\left\{ \begin{array}{l}x = 1 + 3t\\y = - t\\z = t\end{array} \right.\). Mà \(M \in d\)\( \Rightarrow M\left( {1 + 3t; - t;t} \right)\).
Ta có \(\overrightarrow {AM} = \left( {3t - 1; - t - 2;t} \right),\overrightarrow {BM} = \left( {3t - 1; - t;t + 2} \right)\).
Ta có \(\cos \left( {\overrightarrow {AM} ,\overrightarrow {BM} } \right) = \frac{{{{\left( {3t - 1} \right)}^2} + 2\left( {{t^2} + 2t} \right)}}{{{{\left( {3t - 1} \right)}^2} + {t^2} + {{\left( {t + 2} \right)}^2}}}\)
\( = \frac{{11{t^2} - 2t + 1}}{{11{t^2} - 2t + 5}} = 1 - \frac{4}{{11{t^2} - 2t + 5}} = 1 - \frac{4}{{11{{\left( {t - \frac{1}{{11}}} \right)}^2} + \frac{{54}}{{11}}}}\).
Suy ra \(\widehat {AMB}\) lớn nhất khi và chỉ khi \(t = \frac{1}{{11}}\).
Do đó \(M\left( {\frac{{14}}{{11}}; - \frac{1}{{11}};\frac{1}{{11}}} \right)\)\( \Rightarrow S = a + b + c = \frac{{14}}{{11}} \approx 1,27\).
Đáp án: \(1,27\).
Lời giải
Để dân số nước ta vượt 120 triệu người thì: \[98\,\,564\,\,407 \cdot {{\rm{e}}^{0,0093t}} > 120\,\,000\,\,000\]
\[ \Leftrightarrow t > \frac{1}{{0,0093}}\ln \frac{{120\,\,000\,\,000}}{{98\,\,564\,\,407}} \approx 21,16\]nên \[t > 21,16\].
Vậy kể từ năm 2043 trở đi dân số nước ta vượt 120 triệu người.
Đáp án: \(2043\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.