Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của môt nhóm khách như sau 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm một người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15 080 000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ.
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của môt nhóm khách như sau 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm một người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15 080 000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x\) là số lượng khách tính từ người thứ 51 trở lên của nhóm (điều kiện \(x \in \mathbb{N}*\)).
Khi đó số lượng khách tham quan là \(50 + x\).
Thêm \(x\) người thì giá vé sẽ giảm \(5000x\) (đồng).
Khi đó giá vé một người phải trả là \(300000 - 5000x\).
Tổng chi phí của đoàn khách tham quan là \(\left( {50 + x} \right)\left( {300000 - 5000x} \right)\) đồng.
Để công ty không bị lỗ thì \(\left( {50 + x} \right)\left( {300000 - 5000x} \right) \ge 15080000\)
\( \Leftrightarrow - 5000{x^2} + 50000x - 80000 \ge 0\)\( \Leftrightarrow 2 \le x \le 8\).
Do đó số người của nhóm khách nhiều nhất là 58 người thì công ty sẽ không bị lỗ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
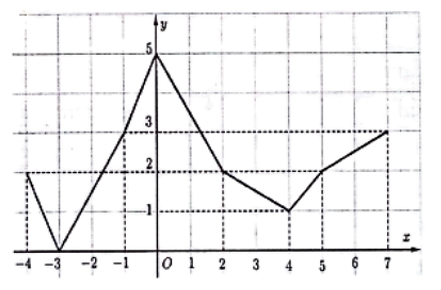
a) Dựa vào đồ thị ta có tập giá trị của hàm số là \(\left[ {0;5} \right]\).
b) Dựa vào đồ thị hàm số ta có hàm số đồng biến trên các khoảng \(\left( { - 3;0} \right)\) và \(\left( {4;7} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) S, b) S, c) Đ, d) Đ
a) Tọa độ đỉnh \(I\) của parabol \({x_I} = - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.1}} = 2;{y_I} = {2^2} - 4.2 + 1 = - 3\).
Suy ra \(I\left( {2; - 3} \right)\).
b) Phương trình trục đối xứng parabol: \(x = 2\).
c) Vì \(a = 1 > 0\) nên bề lõm parabol hướng lên.
d) Ta có bảng giá trị
Ta có đồ thị
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
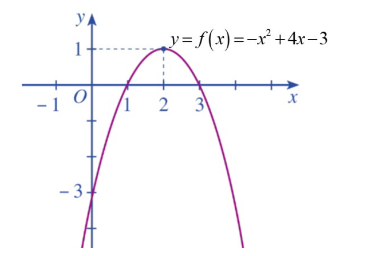
A. \(f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\).
B. \(f\left( x \right) > 0 \Leftrightarrow x \in \left[ {1;3} \right]\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập