Tìm m để phương trình \[{\rm{msi}}{{\rm{n}}^{\rm{2}}}{\rm{x + co}}{{\rm{s}}^{\rm{2}}}{\rm{x = m}} - {\rm{1}}\,\,\left( {\rm{1}} \right)\] có nghiệm trên khoảng\[\left( {{\rm{0; }}\frac{{\rm{\pi }}}{{\rm{4}}}} \right)\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì \[{\rm{cosx = 0}} \Rightarrow {\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm{x = 1}} \Rightarrow \left( 1 \right)\] vô lý nên \[{\rm{co}}{{\rm{s}}^{\rm{2}}}{\rm{x}} \ne 0\]
Ta chia 2 vế của phương trình (1) cho \[{\rm{co}}{{\rm{s}}^{\rm{2}}}{\rm{x}}\], ta được:
\[{\rm{mta}}{{\rm{n}}^{\rm{2}}}{\rm{x + 1 = }}\left( {{\rm{m}} - {\rm{1}}} \right)\left( {{\rm{1 + ta}}{{\rm{n}}^{\rm{2}}}{\rm{x}}} \right) \Leftrightarrow {\mathop{\rm t}\nolimits} {\rm{a}}{{\rm{n}}^{\rm{2}}}{\rm{x = m}} - {\rm{2}}\,\,\left( 2 \right)\]
(1) có nghiệm \[{\rm{x}} \in \left( {{\rm{0; }}\frac{{\rm{\pi }}}{{\rm{4}}}} \right) \Leftrightarrow \] (2) có nghiệm\[{\rm{x}} \in \left( {{\rm{0; }}\frac{{\rm{\pi }}}{{\rm{4}}}} \right) \Leftrightarrow {\rm{m}} - {\rm{2}} \in \left( {0;1} \right) \Leftrightarrow 2 < {\rm{m}} < 3\]
Đáp án cần chọn là: D
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\[{\rm{cosx = cos}}\frac{{\rm{\pi }}}{{{\rm{12}}}} \Rightarrow \left[ {\begin{array}{*{20}{c}}{{\rm{x = }}\frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{ + k2\pi }}}\\{{\rm{x = }} - \frac{{\rm{\pi }}}{{{\rm{12}}}}{\rm{ + k2\pi }}}\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\]
Đáp án cần chọn là: B
Lời giải
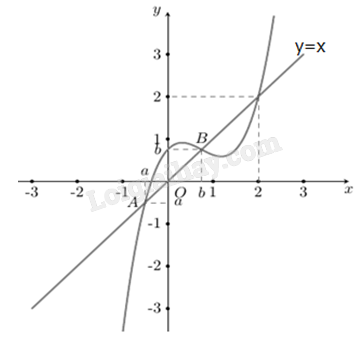
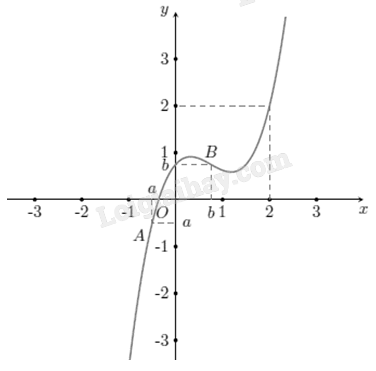
Từ đồ thị ta có\[f(x)\,{\rm{ = }}x \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{\rm{x = a}} \in \left( { - \infty ;0} \right)}\\{{\rm{x = b}} \in \left( {0;1} \right)}\\{{\rm{x = 2}}}\end{array}} \right.\]
Do đó\[{\rm{f(cosx + 1) = cosx + 1}} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{\rm{cosx + 1 = a}} \in \left( { - \infty ;0} \right)}\\{{\rm{cosx + 1 = b}} \in \left( {0;1} \right)}\\{c{\rm{osx + 1 = 2}}}\end{array}} \right.\]
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{co{\rm{sx = a}} - {\rm{1 = }}{{\rm{t}}_{\rm{1}}} \in ( - \infty ; - 1)\,\,(VN)}\\{{\rm{cosx = b}} - {\rm{1 = }}{{\rm{t}}_{\rm{2}}} \in ( - 1;0)\,\,(1)}\\{{\rm{cosx = 1 }}(2)}\end{array}} \right.\)
Dựa vào đường tròn lượng giác, phương trình có 3 nghiệm nằm trong\[\left( {\frac{{ - {\rm{\pi }}}}{2};3{\rm{\pi }}} \right)\]
Phương trình có 2 nghiệm nằm trong\[\left( {\frac{{ - {\rm{\pi }}}}{2};3{\rm{\pi }}} \right)\]
Vậy phương trình ban đầu có tất cả 5 nghiệm nằm trong \[\left( {\frac{{ - {\rm{\pi }}}}{2};3{\rm{\pi }}} \right)\]
Đáp án cần chọn là: C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo