Câu hỏi:
11/03/2025 750
Câu 1- 2. (1,5 điểm)
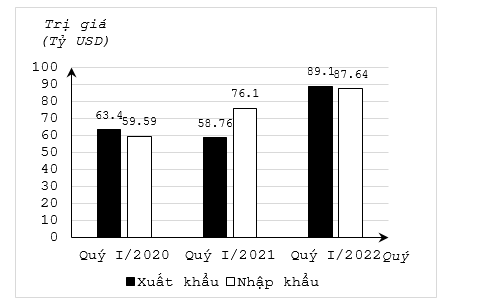
1) Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\).
a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là bao nhiêu tỷ USD?
b) Trị giá xuất khẩu trong quý I/2021 chiếm bao nhiêu phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) (làm tròn đến hàng đơn vị).
Câu 1- 2. (1,5 điểm)
1) Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\).
a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là bao nhiêu tỷ USD?
b) Trị giá xuất khẩu trong quý I/2021 chiếm bao nhiêu phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) (làm tròn đến hàng đơn vị).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là:
\(63,4 + 58,76 + 89,1 = 211,26\) (tỷ USD).
b) Trị giá xuất khẩu trong quý I/2021 chiếm số phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là:
\(\frac{{58,76}}{{211,26}} \cdot 100\% \approx 27,8\% \).
Câu hỏi cùng đoạn
Câu 2:
2) Một hộp có \(25\) chiếc thẻ cùng loại, mỗi thẻ được ghi đúng trong các số \(1;2;3;4;...;25,\) hai thẻ khác nhau ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp” và biến cố N: “Số xuất hiện trên thẻ được rút ra là một số chia hết cho \(5\)”. Tính xác suất biến cố N.
Lời giải của GV VietJack
Không gian mẫu của phép thử rút ngẫu nhiên một thẻ trong hộp là: \(\Omega = \left\{ {1;\,\,2;\,\,3,\,\,...;\,\,25} \right\}\)
Không gian mẫu có \(25\)phần tử.
Biến cố N: “Số xuất hiện trên thẻ được rút ra là một số chia hết cho \(5\)” có 5 kết quả thuận lợi là \(5;\,\,10;\,\,15;\,\,20;\,\,25.\)
Vậy xác suất của biến cố \[N\] là: \(P\left( N \right) = \frac{5}{{25}} = \frac{1}{5}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
1) Nếu hai vòi nước cùng chảy vào một bể (không chứa nước) thì sau \[1\] giờ \[20\] phút đầy bể. Nếu mở vòi thứ nhất chảy trong \[10\] phút rồi khóa lại, vòi thứ hai chảy tiếp trong \[12\] phút thì được \(\frac{2}{{15}}\) bể. Hỏi nếu mỗi vòi chảy riêng thì sau bao lâu sẽ đầy bể?
Xem đáp án »
11/03/2025
228
Câu 3:
(0,5 điểm) Cho tam giác đều có độ dài cạnh bằng Bạn Nam cắt một hình chữ nhật sao cho thuộc lần lượt thuộc Đặt cạnh Tìm để diện tích hình chữ nhật lớn nhất.
Xem đáp án »
11/03/2025
221
Câu 5:
1) Cùng với cây đa, sân đình, từ bao đời nay, giếng làng đã trở thành một trong những biểu tượng vẻ đẹp của vùng quê Việt Nam, đặc biệt là ở đồng bằng Bắc Bộ. Giếng làng chính là nơi chứng kiến bao sự kiện của làng xóm từ thế hệ này qua thế hệ khác. Hiện nay, tại làng Trung Kính Thượng, phường Trung Hòa vẫn đang lưu giữ một chiếc giếng cổ (Hình 1). Biết nắp giếng có dạng hình tròn với bán kính \[55\,{\rm{cm}}\], miệng giếng là hình vành khăn có độ dày \[{\rm{10}}\,{\rm{cm}}\] (Hình 2).
a) Tính diện tích phần nắp giếng có dạng hình tròn (được chú thích như Hình 2).
b) Tính diện tích phần miệng giếng hình vành khăn (phần tô đậm trên Hình 2).(Lấy \(\pi \approx 3,14).\)
a) Tính diện tích phần nắp giếng có dạng hình tròn (được chú thích như Hình 2).
b) Tính diện tích phần miệng giếng hình vành khăn (phần tô đậm trên Hình 2).(Lấy \(\pi \approx 3,14).\)
Xem đáp án »
11/03/2025
91
Câu 6:
2) Một hộp có \(25\) chiếc thẻ cùng loại, mỗi thẻ được ghi đúng trong các số \(1;2;3;4;...;25,\) hai thẻ khác nhau ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp” và biến cố N: “Số xuất hiện trên thẻ được rút ra là một số chia hết cho \(5\)”. Tính xác suất biến cố N.
Xem đáp án »
11/03/2025
0
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
-
123 bài tập Nón trụ cầu và hình khối có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận