Câu hỏi:

11/03/2025 902

Câu 3-5 (1,5 điểm)

Cho hai biểu thức $A = \frac{\sqrt{x} + 3}{3 - \sqrt{x}}$ và $B = \frac{\sqrt{x}}{\sqrt{x} + 3} + \frac{2 \sqrt{x}}{\sqrt{x} - 3} - \frac{3 x + 9}{x - 9}$ với $x \geq 0; x \neq 9$ .

1) Tính giá trị của A biểu thức khi x=16.

Xem lời giải

Câu hỏi trong đề: Đề thi thử TS vào 10 (Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Yên Hòa_Quận Cầu Giấy !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Thay $x = 16$ (thỏa mãn) vào biểu thức $A,$ ta được:

\[A = \frac{{\sqrt {16} + 3}}{{3 - \sqrt {16} }} = \frac{{4 + 3}}{{3 - 4}} = - 7.\]

Vậy $A = - 7$ khi $x = 16.$

Câu hỏi cùng đoạn

Câu 2:

2) Rút gọn B.

Xem lời giải

Lời giải của GV VietJack

Với $x \ge 0;\,\,x \ne 9$, ta có:

$B = \frac{{\sqrt x }}{{\sqrt x + 3}} + \frac{{2\sqrt x }}{{\sqrt x - 3}} - \frac{{3x + 9}}{{x - 9}}$

$ = \frac{{\sqrt x \left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} + \frac{{2\sqrt x \left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}} - \frac{{3x + 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}$

$ = \frac{{x - 3\sqrt x + 2x + 6\sqrt x - 3x - 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}$$ = \frac{{3\sqrt x - 9}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}$

$ = \frac{{3\left( {\sqrt x - 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}$$ = \frac{3}{{\sqrt x + 3}}.$

Vậy với $x \ge 0;\,\,x \ne 9$ thì $B = \frac{3}{{\sqrt x + 3}}.$

Câu 3:

3) Tìm các giá trị của x sao cho $AB \leq 1$ .

Xem lời giải

Lời giải của GV VietJack

Với $x \ge 0;\,\,x \ne 9$, ta có:

\[AB = \frac{{\sqrt x + 3}}{{3 - \sqrt x }} \cdot \frac{3}{{\sqrt x + 3}} = \frac{3}{{3 - \sqrt x }}.\]

Theo bài, $AB \le 1$ nên $\frac{3}{{3 - \sqrt x }} \le 1$

Hay $\frac{{ - 3}}{{\sqrt x - 3}} \le 1$

$1 + \frac{3}{{\sqrt x - 3}} \ge 0$

$\frac{{\sqrt x - 3 + 3}}{{\sqrt x - 3}} \ge 0$

$\frac{{\sqrt x }}{{\sqrt x - 3}} \ge 0.\,\,\,\left( * \right)$

Trường hợp 1: Nếu $x = 0,$ ta có $\sqrt x = 0$ và $\sqrt x - 3 = - 3 \ne 0$ nên $\frac{{\sqrt x }}{{\sqrt x - 3}} = 0$ nên $x = 0$ là một nghiệm của bất phương trình (*0.

Trường hợp 2: Nếu $x > 0,\,\,x \ne 9$ thì $\sqrt x > 0$ nên giải bất phương trình (*) ta có:

$\sqrt x - 3 > 0$ hay $\sqrt x > 3$ suy ra $x > 9.$

Kết hợp với điều kiện $x \ge 0;\,\,x \ne 9$ ta có $x > 9.$

Vậy $x = 0$ và $x > 9$ thì $A.B \le 1$.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

1) Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn $2020 - 2022$.

$a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn $2020 - 2022$ là bao nhiêu tỷ USD? (ảnh 1)$

a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn $2020 - 2022$ là bao nhiêu tỷ USD?

b) Trị giá xuất khẩu trong quý I/2021 chiếm bao nhiêu phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn $2020 - 2022$ (làm tròn đến hàng đơn vị).

Xem đáp án

Lời giải

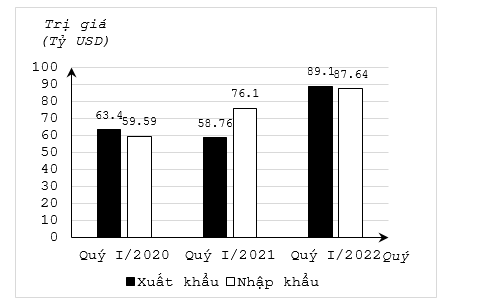
a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn $2020 - 2022$ là:

$63,4 + 58,76 + 89,1 = 211,26$ (tỷ USD).

b) Trị giá xuất khẩu trong quý I/2021 chiếm số phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn $2020 - 2022$ là:

$\frac{{58,76}}{{211,26}} \cdot 100\% \approx 27,8\% $.

Câu 2

(0,5 điểm) Cho tam giác đều $A B C$ có độ dài cạnh bằng $20 c m .$ Bạn Nam cắt một hình chữ nhật $M N P Q$ sao cho $M, N$ thuộc $B C; P, Q$ lần lượt thuộc $A C, A B .$ Đặt cạnh $M N = P Q = x .$ Tìm $x$ để diện tích hình chữ nhật $M N P Q$ lớn nhất.

Xem đáp án

Lời giải

Vì $A B C$ là tam giác đều cạnh $20 c m$ nên $B C = 20 c m$ và $\hat{B} = \hat{C} = 60^{\circ} .$

Xét $Δ B M Q$ vuông tại $M$ có $\hat{B} + \hat{B Q M} = 90^{\circ}$ và $Δ C N P$ vuông tại $N$ có $\hat{C} + \hat{C P N} = 90^{\circ}$

Suy ra $\hat{B Q M} = \hat{C P N} .$

Vì $M N P Q$ là hình chữ nhật nên $Q M = P N .$

Xét $Δ B M Q$ và $Δ C N P$ có: $\hat{B M Q} = \hat{C N P} = 90^{\circ},$ $Q M = P N$ và $\hat{B Q M} = \hat{C P N} .$

Do đó $Δ B M Q = Δ C N P$ (cạnh góc vuông – góc nhọn kề).

Suy ra $B M = C N$ (hai cạnh tương ứng).

Do $B C = 20 c m$ và $M N = x (c m)$ nên $B M = C N = \frac{20 - x}{2} (c m)$ $(0 < x < 20) .$

Xét $Δ B M Q$ vuông tại $M$ có $Q M = B M \cdot \tan B = \frac{20 - x}{2} \cdot \tan 60^{\circ} = \frac{\sqrt{3} (20 - x)}{2} (c m) .$

Diện tích hình chữ nhật $M N P Q$ là: $S = Q M \cdot M N = \frac{\sqrt{3} (20 - x)}{2} \cdot x = \frac{\sqrt{3}}{x} (20 x - x^{2}) (c m^{2}) .$

Để diện tích hình chữ nhật $M N P Q$ lớn nhất thì ta tìm giá trị lớn nhất của biểu thức $S .$

Ta có $S = \frac{\sqrt{3}}{2} (20 x - x^{2}) = \frac{\sqrt{3}}{2} (20 x - x^{2} - 100 + 100)$

$= \frac{\sqrt{3}}{2} [100 - {(x - 10)}^{2}] = 50 \sqrt{3} - \frac{\sqrt{3}}{2} {(x - 10)}^{2} .$

Với mọi $0 < x < 20$ ta có ${(x - 10)}^{2} \geq 0$ nên $50 \sqrt{3} - \frac{\sqrt{3}}{2} {(x - 10)}^{2} \leq 50 \sqrt{3}$ hay $S \leq 50 \sqrt{3} .$

Dấu “=” xảy ra khi và chỉ khi ${(x - 10)}^{2} = 0,$ hay $x = 10$ (thỏa mãn).

Vậy diện tích hình chữ nhật $M N P Q$ lớn nhất bằng $50 \sqrt{3}$ khi $x = 10.$

Câu 3

1) Nếu hai vòi nước cùng chảy vào một bể (không chứa nước) thì sau \[1\] giờ \[20\] phút đầy bể. Nếu mở vòi thứ nhất chảy trong \[10\] phút rồi khóa lại, vòi thứ hai chảy tiếp trong \[12\] phút thì được $\frac{2}{{15}}$ bể. Hỏi nếu mỗi vòi chảy riêng thì sau bao lâu sẽ đầy bể?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

1) Cùng với cây đa, sân đình, từ bao đời nay, giếng làng đã trở thành một trong những biểu tượng vẻ đẹp của vùng quê Việt Nam, đặc biệt là ở đồng bằng Bắc Bộ. Giếng làng chính là nơi chứng kiến bao sự kiện của làng xóm từ thế hệ này qua thế hệ khác. Hiện nay, tại làng Trung Kính Thượng, phường Trung Hòa vẫn đang lưu giữ một chiếc giếng cổ (Hình 1). Biết nắp giếng có dạng hình tròn với bán kính \[55\,{\rm{cm}}\], miệng giếng là hình vành khăn có độ dày \[{\rm{10}}\,{\rm{cm}}\] (Hình 2).

a) Tính diện tích phần nắp giếng có dạng hình tròn (được chú thích như Hình 2).
b) Tính diện tích phần miệng giếng hình vành khăn (phần tô đậm trên Hình 2).(Lấy $\pi \approx 3,14).$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

a) Chứng minh tứ giác \[BCEF\] nội tiếp.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

2) Một hộp có $25$ chiếc thẻ cùng loại, mỗi thẻ được ghi đúng trong các số $1;2;3;4;...;25,$ hai thẻ khác nhau ghi hai số khác nhau. Xét phép thử “Rút ngẫu nhiên một thẻ trong hộp” và biến cố N: “Số xuất hiện trên thẻ được rút ra là một số chia hết cho $5$”. Tính xác suất biến cố N.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Câu 3-5 (1,5 điểm) Cho hai biểu thức A=x+33−x và B=xx+3+2xx−3−3x+9x−9 với x≥0; x≠9 . 1) Tính giá trị của A biểu thức khi x=16.

2) Rút gọn B.

3) Tìm các giá trị của x sao cho AB≤1 .

Bình luận

(0,5 điểm) Cho tam giác đều ABC có độ dài cạnh bằng 20cm. Bạn Nam cắt một hình chữ nhật MNPQ sao cho M,N thuộc BC;P,Q lần lượt thuộc AC,AB. Đặt cạnh MN=PQ=x. Tìm x để diện tích hình chữ nhật MNPQ lớn nhất.

a) Chứng minh tứ giác \[BCEF\] nội tiếp.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Câu 3-5 (1,5 điểm)

Cho hai biểu thức $A = \frac{\sqrt{x} + 3}{3 - \sqrt{x}}$ và $B = \frac{\sqrt{x}}{\sqrt{x} + 3} + \frac{2 \sqrt{x}}{\sqrt{x} - 3} - \frac{3 x + 9}{x - 9}$ với $x \geq 0; x \neq 9$ .

1) Tính giá trị của A biểu thức khi x=16.

3) Tìm các giá trị của x sao cho $AB \leq 1$ .