Câu 10-12. (4,0 điểm)
Cho \(\Delta ABC\) nhọn \[\left( {AB > AC} \right)\] nội tiếp đường tròn \[\left( {O;R} \right).\] Đường cao \[BE,\] \[CF\] cắt nhau tại \[H.\] Lấy \[M\] là trung điểm \[BC.\]
a) Chứng minh tứ giác \[BCEF\] nội tiếp.
Câu 10-12. (4,0 điểm)
Quảng cáo
Trả lời:

a) Có \(BE\) và \(CF\) là hai đường cao của tam giác \(ABC\) nên \(BE \bot AC;\,\,CF \bot AB.\)
Suy ra \(\widehat {BEA} = \widehat {BEC} = 90^\circ \) và \(\widehat {CFA} = \widehat {CFB} = 90^\circ .\)
Xét \(\Delta BFC\) vuông tại \(F\) có \(FM\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên \(MF = MB = MC = \frac{{BC}}{2}.\)
Chứng minh tương tự, ta có:
\(ME = MB = MC = \frac{{BC}}{2}.\)
Suy ra \(ME = MF = MB = MC = \frac{{BC}}{2}.\)Vậy bốn điểm \(B,\,\,F,\,\,E,\,\,C\) cùng thuộc đường tròn \(\left( {M;\,\,\frac{{BC}}{2}} \right)\) hay tứ giác \(BCEF\) nội tiếp đường tròn \(\left( {M;\,\,\frac{{BC}}{2}} \right).\)
Câu hỏi cùng đoạn
Câu 2:
b) Đường thẳng \[AM\] cắt đường tròn \[\left( O \right)\] tại điểm thứ hai là \[D.\] Chứng minh \(OM \bot BC\) và \(M{B^2} = MA \cdot MD.\)
⦁ Xét \(\Delta OBC\) cân tại \(O\) (do \(OB = OC)\) nên đường trung tuyến \(OM\) đồng thời là đường cao của tam giác, hay \(OM \bot BC\) tại \(M.\)
⦁ Xét đường tròn \(\left( O \right)\) có \[\widehat {BAD} = \widehat {BCD}\] (hai góc nội tiếp cùng chắn cung \(BD)\) hay \(\widehat {MAB} = \widehat {MCD}.\)
Xét \(\Delta MAB\) và \(\Delta MCD\) có: \(\widehat {AMB} = \widehat {CMD}\) (đối đỉnh) và \(\widehat {MAB} = \widehat {MCD}.\)
Do đó (g.g). Suy ra: \(\frac{{MA}}{{MC}} = \frac{{MB}}{{MD}}\) hay \(MB \cdot MC = MA \cdot MD.\)
Mà \(MB = MC\) nên suy ra: \(M{B^2} = MA \cdot MD.\)
Câu 3:
c) Kẻ đường kính \(AK\) của \(\left( O \right).\) Chứng minh \(OM = \frac{1}{2}AH.\)
Xét đường tròn \(\left( O \right)\) có \[\widehat {ACK} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn), suy ra \(KC \bot AC.\)
Lại có \(BE \bot AC\) nên \[BE\,{\rm{//}}\,KC\] hay \[BH\,{\rm{//}}\,KC.\]
Chứng minh tương tự, ta có \(KB\,{\rm{//}}\,CH.\)
Tứ giác \(BHCK\) có \[BH\,{\rm{//}}\,KC\] và \(KB\,{\rm{//}}\,CH\) nên là hình bình hành, do đó hai đường chéo \(BC,\,\,HK\) cắt nhau tại trung điểm của mỗi đường.
Mà \(M\) là trung điểm của \(BC\) nên \(M\) cũng là trung điểm của \(HK.\)
Xét \(\Delta AHK\) có \(O,\,\,M\) lần lượt là trung điểm của \(AK,\,\,HK\) nên \(OM\) là đường trung bình của tam giác. Suy ra \(OM = \frac{1}{2}AH.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Thay \(x = 16\) (thỏa mãn) vào biểu thức \(A,\) ta được:
\[A = \frac{{\sqrt {16} + 3}}{{3 - \sqrt {16} }} = \frac{{4 + 3}}{{3 - 4}} = - 7.\]
Vậy \(A = - 7\) khi \(x = 16.\)
Lời giải
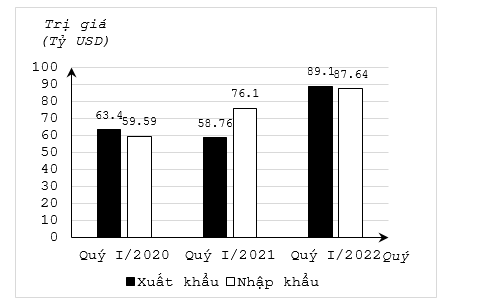
a) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là:
\(63,4 + 58,76 + 89,1 = 211,26\) (tỷ USD).
b) Trị giá xuất khẩu trong quý I/2021 chiếm số phần trăm so với tổng trị trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn \(2020 - 2022\) là:
\(\frac{{58,76}}{{211,26}} \cdot 100\% \approx 27,8\% \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.