Câu hỏi:
11/03/2025 151
Câu 9-11: (3 điểm)
Cho đường tròn \[\left( O \right)\] với đường kính \[AC.\] Trên đoạn \[OC\] lấy điểm \[B\]. Gọi \[M\] là trung điểm \[AB,\] từ \[M\] kẻ dây \[DE\] vuông góc với \[AB.\] Từ \[B\] kẻ \[BF\] vuông góc với \[CD\] \[\left( {F \in CD} \right).\]
a) Chứng minh tứ giác \[BMDF\] nội tiếp.
Câu 9-11: (3 điểm)
Cho đường tròn \[\left( O \right)\] với đường kính \[AC.\] Trên đoạn \[OC\] lấy điểm \[B\]. Gọi \[M\] là trung điểm \[AB,\] từ \[M\] kẻ dây \[DE\] vuông góc với \[AB.\] Từ \[B\] kẻ \[BF\] vuông góc với \[CD\] \[\left( {F \in CD} \right).\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
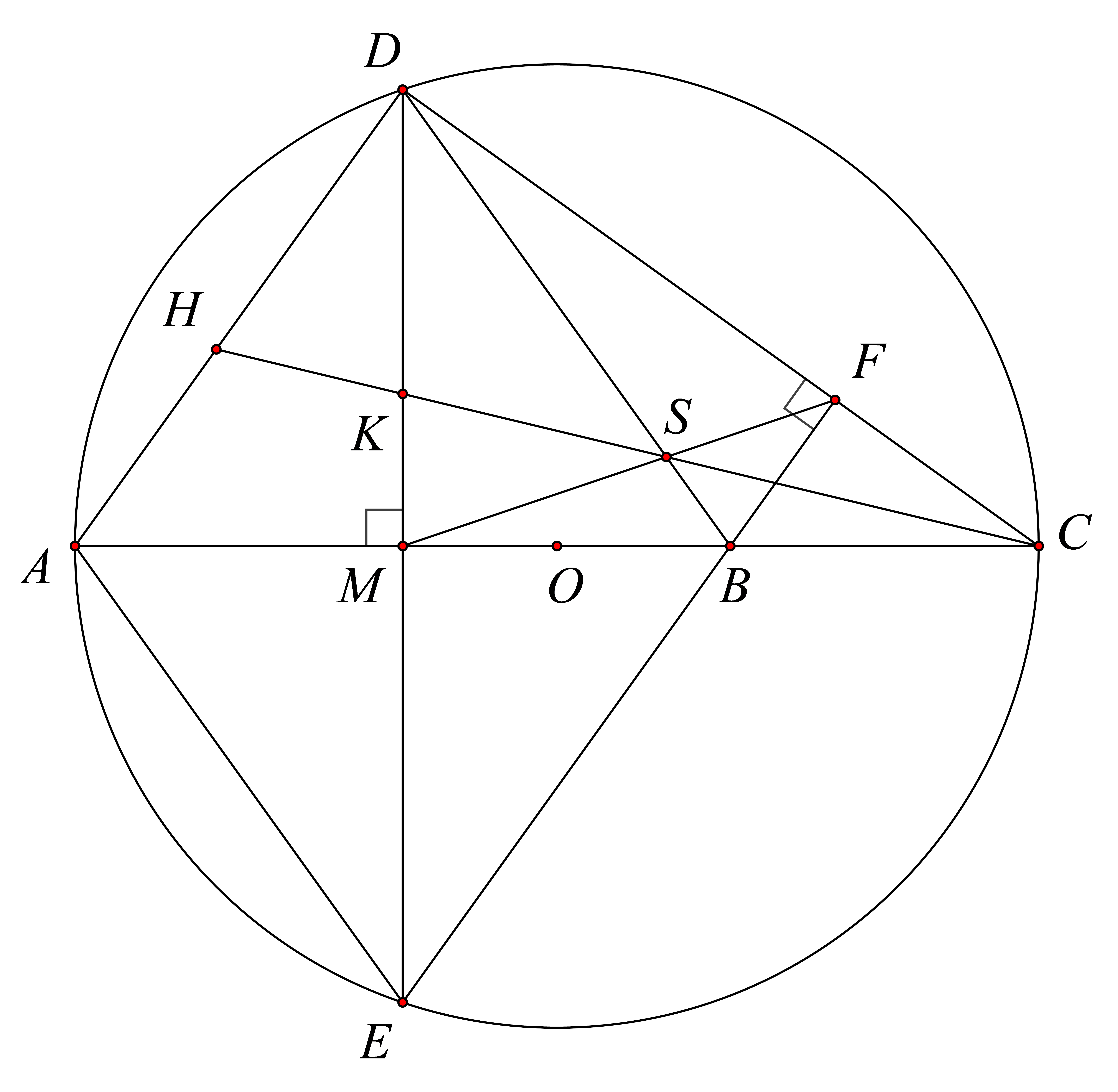
a) Ta có \(\Delta DMB\) vuông tại \(M\) nên ba điểm \(M,\,\,D,\,\,B\) thuộc đường tròn đường kính \(DB.\) (1)
Do \(\Delta DFB\) vuông tại \(F\) nên ba điểm \(F,\,\,D,\,\,B\) thuộc đường tròn đường kính \(DB.\) (2)
Từ (1) và (2) suy ra bốn điểm \(M,\,\,D,\,\,B,\,\,F\) cùng thuộc một đường tròn đường kính \(DB.\)
Do đó tứ giác \[BMDF\] nội tiếp đường kính \(DB.\)
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn với đường kính Trên đoạn lấy điểm . Gọi là trung điểm từ kẻ dây vuông góc với Từ kẻ vuông góc với
Lời giải của GV VietJack
⦁ Xét cân tại có là đường cao nên đồng thời là đường trung tuyến của tam giác.
Do đó là trung điểm của
Xét tứ giác có là trung điểm của hai đường chéo nên là hình bình hành.
Lại có nên tứ giác là hình thoi.
⦁ Xét đường tròn có (góc nội tiếp chắn nửa đường tròn) nên
Do tứ giác là hình thoi nên suy ra
Mà suy ra ba điểm thẳng hàng.
Xét vuông tại có là trung tuyến ứng với cạnh huyền nên (3)
Xét và có: và (cùng phụ với
Do đó (g.g). Suy ra hay
Mà (do là trung điểm của suy ra (4)
Từ (3) và (4) suy ra
Câu 3:
c) Gọi \[S\] là giao điểm của \[BD\] với \[MF,\] tia \[CS\] lần lượt cắt \[AD,\] \[DE\] tại \[H\] và \[K.\] Chứng minh: \[\frac{{DA}}{{DH}} + \frac{{DB}}{{DS}} = \frac{{DE}}{{DK}}.\]
Lời giải của GV VietJack
![Chứng minh: \[\frac{{DA}}{{DH}} + \frac{{DB}}{{DS}} = \frac{{DE}}{{DK}}.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/16-1741697241.png)
Kẻ \[AJ\,{\rm{//}}\,HK\] và \[BI\,{\rm{//}}\,HK\] \[\left( {I,\,\,J \in DE} \right).\]
Theo định lí Thalès, ta có: \(\frac{{DA}}{{DH}} = \frac{{DJ}}{{DK}};\,\,\frac{{DB}}{{DS}} = \frac{{DI}}{{DK}}.\)
Suy ra \(\frac{{DA}}{{DH}} + \frac{{DB}}{{DS}} = \frac{{DJ}}{{DK}} + \frac{{DI}}{{DK}} = \frac{{DJ + DI}}{{DK}}\) (5)
Do \[AJ\,{\rm{//}}\,HK\] và \[BI\,{\rm{//}}\,HK\] nên \(AJ\,{\rm{//}}\,BI\) suy ra \(\widehat {MBI} = \widehat {MAJ}\) (so le trong).
Xét \[\Delta BIM\] và \(\Delta AJM\) có:
\(\widehat {BMI} = \widehat {AMJ} = 90^\circ ,\) \(MA = MB,\) \(\widehat {MBI} = \widehat {MAJ}\)Do đó \[\Delta BIM = \Delta AJM\] (cạnh góc vuông – góc nhọn kề). Suy ra \(MI = MJ\) (hai cạnh tương ứng).
Lại có \(MD = ME\) nên \(MD - MI = ME - MJ\) hay \(DI = EJ\) (6)
Từ (5) và (6) suy ra \(\frac{{DA}}{{DH}} + \frac{{DB}}{{DS}} = \frac{{DJ + JE}}{{DK}} = \frac{{DE}}{{DK}}.\)
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Nếu người ta làm hàng rào xung quanh công viên thì hàng rào có chiều dài bao nhiêu?
Xem đáp án »
11/03/2025
1,257
Câu 2:
1) Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được \[600\] tấn thóc. Năm nay, đơn vị thứ nhất làm vượt mức \(10{\rm{\% }}\), đơn vị thứ hai làm vượt mức \(20{\rm{\% }}\) so với năm ngoái. Do đó cả hai đơn vị thu hoạch được \[685\] tấn thóc. Hỏi năm ngoái, mỗi đơn vị thu hoạch được bao nhiêu tấn thóc?
Xem đáp án »
11/03/2025
211
Câu 4:
(0,5 điểm) Xét các hình hộp chữ nhật có thể tích bằng \(27\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\) mà đáy là hình vuông cạnh \(a\,\,({\rm{cm}})\) và chiều cao \(h\,\,({\rm{cm}}).\) Tìm hình hộp có diện tích toàn phần nhỏ nhất.
(0,5 điểm) Xét các hình hộp chữ nhật có thể tích bằng \(27\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\) mà đáy là hình vuông cạnh \(a\,\,({\rm{cm}})\) và chiều cao \(h\,\,({\rm{cm}}).\) Tìm hình hộp có diện tích toàn phần nhỏ nhất.
Xem đáp án »
11/03/2025
163
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận