(1,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Trong đợt thi đấu giải bóng bàn dành cho lứa tuổi học sinh THCS của năm học 2024 – 2025. Một đội tuyển học sinh của một cụm trường THCS tham gia cuộc thi đấu bóng bàn gồm cả Nam và Nữ. Trong lớp có \(\frac{1}{2}\) số học sinh nam và \(\frac{5}{8}\) số học sinh nữ thi đấu tạo thành cặp (một nam kết hợp với một nữ). Số học sinh còn lại không thi đấu là 16 học sinh làm cổ động viên. Hỏi đội tuyển có tất cả bao nhiêu học sinh?
(1,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Trong đợt thi đấu giải bóng bàn dành cho lứa tuổi học sinh THCS của năm học 2024 – 2025. Một đội tuyển học sinh của một cụm trường THCS tham gia cuộc thi đấu bóng bàn gồm cả Nam và Nữ. Trong lớp có \(\frac{1}{2}\) số học sinh nam và \(\frac{5}{8}\) số học sinh nữ thi đấu tạo thành cặp (một nam kết hợp với một nữ). Số học sinh còn lại không thi đấu là 16 học sinh làm cổ động viên. Hỏi đội tuyển có tất cả bao nhiêu học sinh?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi số học sinh nam và nữ của đội tuyển lần lượt là \(x,\;y\) (học sinh)\(\left( {x,\,\,y \in {\mathbb{N}^*}} \right).\)
\(\frac{1}{2}\) số học sinh nam của đội tuyển là: \(\frac{1}{2}x\) (học sinh).
\(\frac{5}{8}\) số học sinh nữ của đội tuyển là: \(\frac{5}{8}y\) (học sinh).
Thi đấu theo cặp thì số học sinh nam thi đấu bằng số học sinh nữ thi đấu nên ta có phương trình: \(\frac{1}{2}x = \frac{5}{8}y\) hay \(4x = 5y\) nên \(4x - 5y = 0.\) (1)
Số học sinh nam còn lại để cổ vũ là: \(x - \frac{1}{2}x = \frac{1}{2}x\) (học sinh).
Số học sinh nữ còn lại để cổ vũ là: \(y - \frac{5}{8}y = \frac{3}{8}y\) (học sinh).
Theo bài, số học sinh còn lại không thi đấu là 16 học sinh nên ta có phương trình:
\(\frac{1}{2}x + \frac{3}{8}y = 16\) hay \(4x + 3y = 128.\) (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}4x - 5y = 0\,\,\,\,\,\,\,\,\left( 1 \right)\\4x + 3y = 128\,\,\,\left( 2 \right)\end{array} \right.\)
Trừ từng vế của phương trình (1) cho phương trình (2), ta được phương trình:
\( - 8y = - 128\) suy ra \(y = 16\) (thỏa mãn).
Thay \(y = 16\) vào phương trình (1), ta được:
\[4x - 5 \cdot 16 = 0\] suy ra \(4x = 80\) nên \(x = 20\) (thỏa mãn).
Vậy đội tuyển có tất cả \(20 + 16 = 36\) học sinh.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Với \(a > 0,\,\,a \ne 1,\) ta có:
\(A = \left( {\frac{{\sqrt a }}{{\sqrt a - 1}} + \frac{1}{{\sqrt a - a}}} \right):\left( {\frac{1}{{\sqrt a + 1}} + \frac{2}{{a - 1}}} \right)\)
\[ = \left[ {\frac{{\sqrt a }}{{\sqrt a - 1}} - \frac{1}{{\sqrt a \left( {\sqrt a - 1} \right)}}} \right]:\left[ {\frac{1}{{\sqrt a + 1}} + \frac{2}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\]
\( = \left[ {\frac{{\sqrt a \cdot \sqrt a }}{{\sqrt a \left( {\sqrt a - 1} \right)}} - \frac{1}{{\sqrt a \left( {\sqrt a - 1} \right)}}} \right]:\left[ {\frac{{\sqrt a - 1}}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}} + \frac{2}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}} \right]\)
\( = \frac{{a - 1}}{{\sqrt a \left( {\sqrt a - 1} \right)}}:\frac{{\sqrt a - 1 + 2}}{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}\)
\( = \frac{{a - 1}}{{\sqrt a \left( {\sqrt a - 1} \right)}} \cdot \frac{{\left( {\sqrt a + 1} \right)\left( {\sqrt a - 1} \right)}}{{\sqrt a + 1}}\)
\( = \frac{{a - 1}}{{\sqrt a }}.\)
Vậy với \(a > 0,\,\,a \ne 1\) thì \(A = \frac{{a - 1}}{{\sqrt a }}.\)
Câu 2
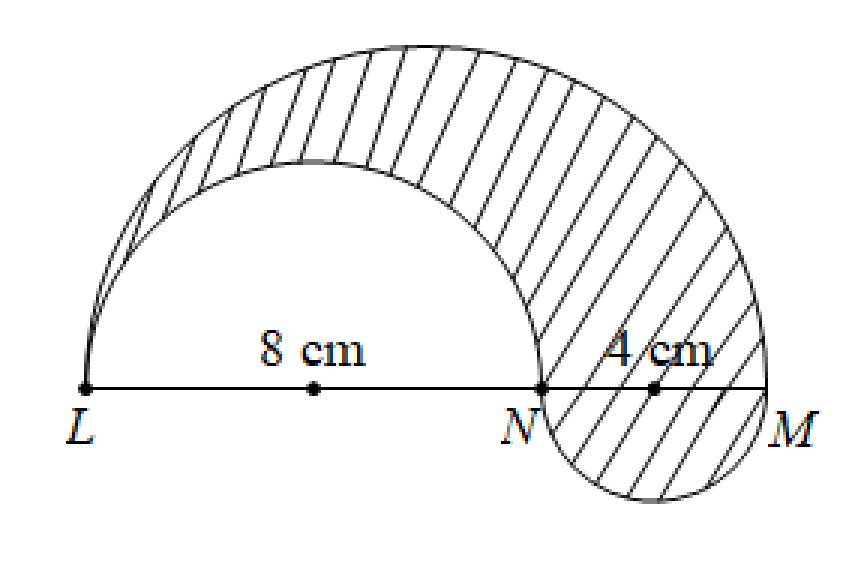
A. \(24\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
B. \(12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có: \(LM = LN + NM = 8 + 4 = 12{\rm{\;(cm)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(LN\) là: \({S_1} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{8}{2}} \right)^2} = 8\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(LM\) là: \({S_2} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{{12}}{2}} \right)^2} = 18\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích nửa hình tròn đường kính \(NM\) là: \({S_3} = \frac{1}{2} \cdot \pi \cdot {\left( {\frac{4}{2}} \right)^2} = 2\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích phần kẻ sọc ở hình đã cho là: \(S = {S_2} - {S_1} + {S_3} = 18\pi - 8\pi + 2\pi = 12\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập