Bên trong một bể cá hình trụ bằng kính người ta đo được chiều cao là 50 cm và đường kính đáy là 20 cm (như hình vẽ). Người ta đổ nước vào bể đến khi mực nước trong bể cách mặt bể 10 cm thì dừng lại sau đó trang trí và thả cá vào bể. Tính thể tích nước đã đổ vào bể (kết quả tính theo đơn vị \({\rm{c}}{{\rm{m}}^3}\) và làm tròn đến chữ số thập phân thứ nhất).
A. \(3\;141,6\;\;{\rm{c}}{{\rm{m}}^3}\).
B. \(15\;708,0\;\;{\rm{c}}{{\rm{m}}^3}\).
C. \(12\;566,4\;\;{\rm{c}}{{\rm{m}}^3}\).
D. \(12\;566,3\;\;{\rm{c}}{{\rm{m}}^3}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Chiều cao (mực nước) của nước đã đổ vào bể trước khi trang trí và thả cá vào bể là:
\(50 - 10 = 40{\rm{\;(cm)}}{\rm{.}}\)
Bán kính đáy của bể là: \(\frac{{20}}{2} = 10{\rm{\;(cm)}}{\rm{.}}\)
Thể tích nước đã đổ vào bể là: \[\pi \cdot {10^2} \cdot 40 = 4\,000\pi \approx 12\;566,4\;{\rm{\;(c}}{{\rm{m}}^3}{\rm{)}}{\rm{.}}\]
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để đồ thị của hàm số \(y = \left( {m - 1} \right){x^2}\,\,\left( {m \ne 1} \right)\) đi qua điểm \(A\left( { - 1;2} \right)\) thì tọa độ điểm \(A\) thỏa mãn hàm số đó.
Thay \(x = - 1,\,\,y = 2\) vào hàm số \(y = \left( {m - 1} \right){x^2},\) ta được:
\(2 = \left( {m - 1} \right) \cdot {\left( { - 1} \right)^2}\) hay \(m - 1 = 2,\) nên \(m = 3\) (thỏa mãn).
Vậy \(m = 3.\)
Câu 2
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/12-1741763486.png)
A. \[M,{\rm{ }}N,{\rm{ }}P.\]
B. \(M,\,\,P,\,\,N.\)
C. \[P,{\rm{ }}N,{\rm{ }}M.\]
D. \(N,\,\,P,\,\,M\).
Lời giải
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/03/13-1741763442.png)
Hướng dẫn giải
Đáp án đúng là: C
Các cung \(MN,\,\,NP,\,\,PM\) chia đường tròn \(\left( O \right)\) thành ba cung có số đo bằng nhau, suy ra mỗi cung có số đo bằng \[\frac{{360^\circ }}{3} = 120^\circ .\]
Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm \(M,\,\,P,\,\,N.\)Câu 3
A. \(\frac{2}{3}\).
B. \(\frac{3}{5}\).
C. \(\frac{2}{5}\).
D. \(\frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 4 cm.
B. 2 cm.
C. \(4\sqrt 2 \;{\rm{cm}}\).
D. \(\sqrt 2 \;{\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
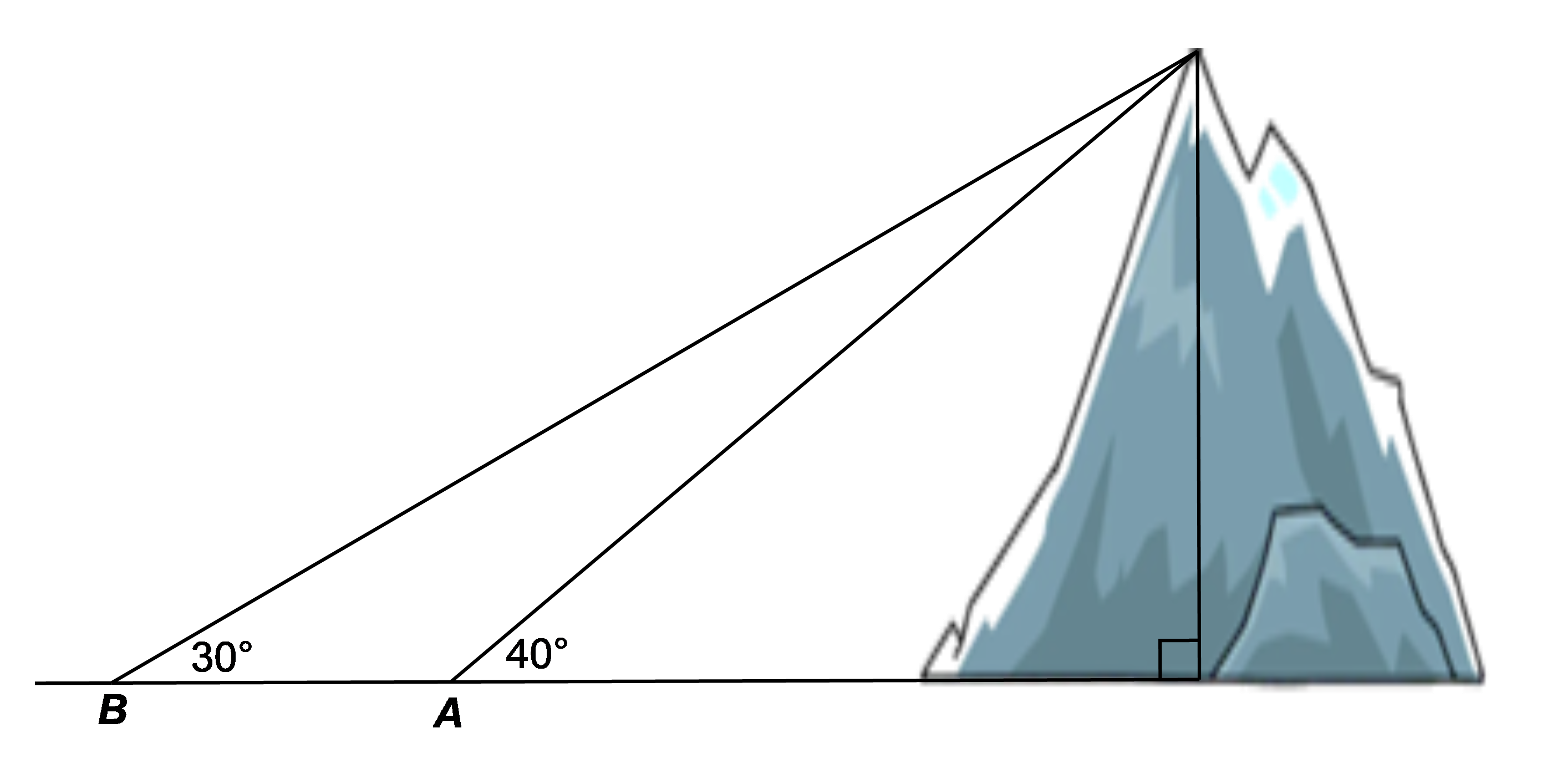
A. 1 110 m.
B. 1 111 m.
C. 1 112 m.
D. 2 292 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[17,4\;\;{\rm{m}}\].
B. \(17,3\;\;{\rm{m}}\).
C. \(17,0\;\;{\rm{m}}\).
D. \(17,32\;\;{\rm{m}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 45 học sinh.
B. 32 học sinh.
C. 40 học sinh.
D. 35 học sinh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo