Câu 28-30: (2,0 điểm) Cho đường tròn \(\left( {O;\,\,R} \right)\) có đường kính \(AB\) cố định. Trên tia đối của tia \(AB\) lấy điểm \(C\) sao cho \(AC = R.\) Qua \(C\) kẻ đường thẳng \(d\) vuông góc với \(CA.\) Lấy điểm \(M\) bất kỳ trên đường tròn \(\left( O \right),\,\,M\) khác \(A\) và \(B\). Tia \(BM\) cắt đường thẳng \(d\) tại \(P.\) Tia \(CM\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(N,\) tia \(PA\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(Q.\)
1) Chứng minh tứ giác \(ACPM\) là tứ giác nội tiếp.
Câu 28-30: (2,0 điểm) Cho đường tròn \(\left( {O;\,\,R} \right)\) có đường kính \(AB\) cố định. Trên tia đối của tia \(AB\) lấy điểm \(C\) sao cho \(AC = R.\) Qua \(C\) kẻ đường thẳng \(d\) vuông góc với \(CA.\) Lấy điểm \(M\) bất kỳ trên đường tròn \(\left( O \right),\,\,M\) khác \(A\) và \(B\). Tia \(BM\) cắt đường thẳng \(d\) tại \(P.\) Tia \(CM\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(N,\) tia \(PA\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(Q.\)
Quảng cáo
Trả lời:

Vì điểm \(M\) nằm trên đường tròn \(\left( O \right)\) đường kính \(AB\) nên \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(\widehat {AMP} = 90^\circ .\)
\(\Delta AMP\) vuông tại \(M\) nên đường tròn ngoại tiếp tam giác có tâm là trung điểm của cạnh huyền \(AP.\) Do đó ba điểm \(A,\,\,M,\,\,P\) cùng nằm trên đường tròn đường kính \(AP.\)
\(\Delta ACP\) vuông tại \(C\) nên đường tròn ngoại tiếp tam giác có tâm là trung điểm của cạnh huyền \(AP.\) Do đó ba điểm \(A,\,\,M,\,\,C\) cùng nằm trên đường tròn đường kính \(AP.\)
Như vậy, bốn điểm \(A,\,\,C,\,\,P,\,\,M\) cùng nằm trên đường tròn đường kính \(AP.\)
Vậy tứ giác \(ACPM\) là tứ giác nội tiếp đường tròn đường kính \(AP.\)
Câu hỏi cùng đoạn
Câu 2:
2) Tính \(BM \cdot BP\) theo \(R.\)
Xét \(\Delta ABM\) và \(\Delta PBC\) có: \(\widehat {AMB} = \widehat {PCB} = 90^\circ \) và \(\widehat {CBP}\) là góc chung
Do đó (g.g). Suy ra \(\frac{{AB}}{{PB}} = \frac{{BM}}{{BC}}\) hay \(BM \cdot BP = AB \cdot BC.\)
Mà \(BC = AB + AC = 2R + R = 3R.\)
Suy ra \(BM \cdot BP = AB \cdot BC = 2R \cdot 3R = 6{R^2}.\)
Câu 3:
3) Gọi \(G\) là trọng tâm của tam giác \(CMB.\) Chứng minh rằng điểm \(G\) luôn nằm trên một đường tròn cố định khi điểm \(M\) thay đổi trên đường tròn \(\left( O \right).\)
Gọi \(K\) là trung điểm của \(BC.\) Khi đó, \(KC = KB.\) (1)
Do \(G\) là trọng tâm của \(\Delta MBC\) nên \(\frac{{MG}}{{MK}} = \frac{2}{3}\) và \(\frac{{KG}}{{KM}} = \frac{1}{3}.\)
Ta có \(KC = KA + CA = KA + R\) và \(KB = KO + OB = KO + R.\) (2)
Từ (1) và (2) suy ra \(KA = KO.\) Do đó \(K\) là trung điểm của \(AO\) nên \(KA = KO = \frac{1}{2}AO.\) (3)
Gọi \(E,\,\,I\) là các điểm thuộc đoạn \(AO\) sao cho \(AE = EI = IO = \frac{1}{3}AO.\) (4)
Từ (3) và (4) suy ra \(\frac{{AE}}{{AK}} = \frac{{\frac{1}{3}AO}}{{\frac{1}{2}AO}} = \frac{2}{3}.\)
Xét \(\Delta AKM\) có \(\frac{{AE}}{{AK}} = \frac{{MG}}{{MK}} = \frac{2}{3}\) nên \(EG\,{\rm{//}}\,AM\) (định lí Thalès đảo).
Lại có \(AM \bot BM\) nên \(EG \bot BM.\) (5)
Ta có \[KB = KO + OB = KO + OA = KO + 2KO = 3KO\] nên \(\frac{{KO}}{{KB}} = \frac{1}{3}.\)
Xét \(\Delta BKM\) có \(\frac{{KO}}{{KB}} = \frac{{KG}}{{KM}} = \frac{1}{3}\) nên \(OG\,{\rm{//}}\,BM\) (định lí Thalès đảo). (6)
Từ (5) và (6) suy ra \(EG \bot OG\) hay \[\widehat {EGO} = 90^\circ .\]
Xét \(\Delta EGO\) vuông tại \(G\) có \(I\) là trung điểm của cạnh huyền \(EO\) nên đường tròn ngoại tiếp \(\Delta EGO\) có tâm là \(I\) và bán kính bằng \(\frac{{EO}}{2}.\)
Do \(AB\) cố định nên \(O,\,\,E,\,\,I\) cố định.
Như vậy, điểm \(G\) nằm trên đường tròn đường kính \(EO\) cố định.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để đồ thị của hàm số \(y = \left( {m - 1} \right){x^2}\,\,\left( {m \ne 1} \right)\) đi qua điểm \(A\left( { - 1;2} \right)\) thì tọa độ điểm \(A\) thỏa mãn hàm số đó.
Thay \(x = - 1,\,\,y = 2\) vào hàm số \(y = \left( {m - 1} \right){x^2},\) ta được:
\(2 = \left( {m - 1} \right) \cdot {\left( { - 1} \right)^2}\) hay \(m - 1 = 2,\) nên \(m = 3\) (thỏa mãn).
Vậy \(m = 3.\)
Câu 2
Lời giải
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/03/13-1741763442.png)
Hướng dẫn giải
Đáp án đúng là: C
Các cung \(MN,\,\,NP,\,\,PM\) chia đường tròn \(\left( O \right)\) thành ba cung có số đo bằng nhau, suy ra mỗi cung có số đo bằng \[\frac{{360^\circ }}{3} = 120^\circ .\]
Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm \(M,\,\,P,\,\,N.\)Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
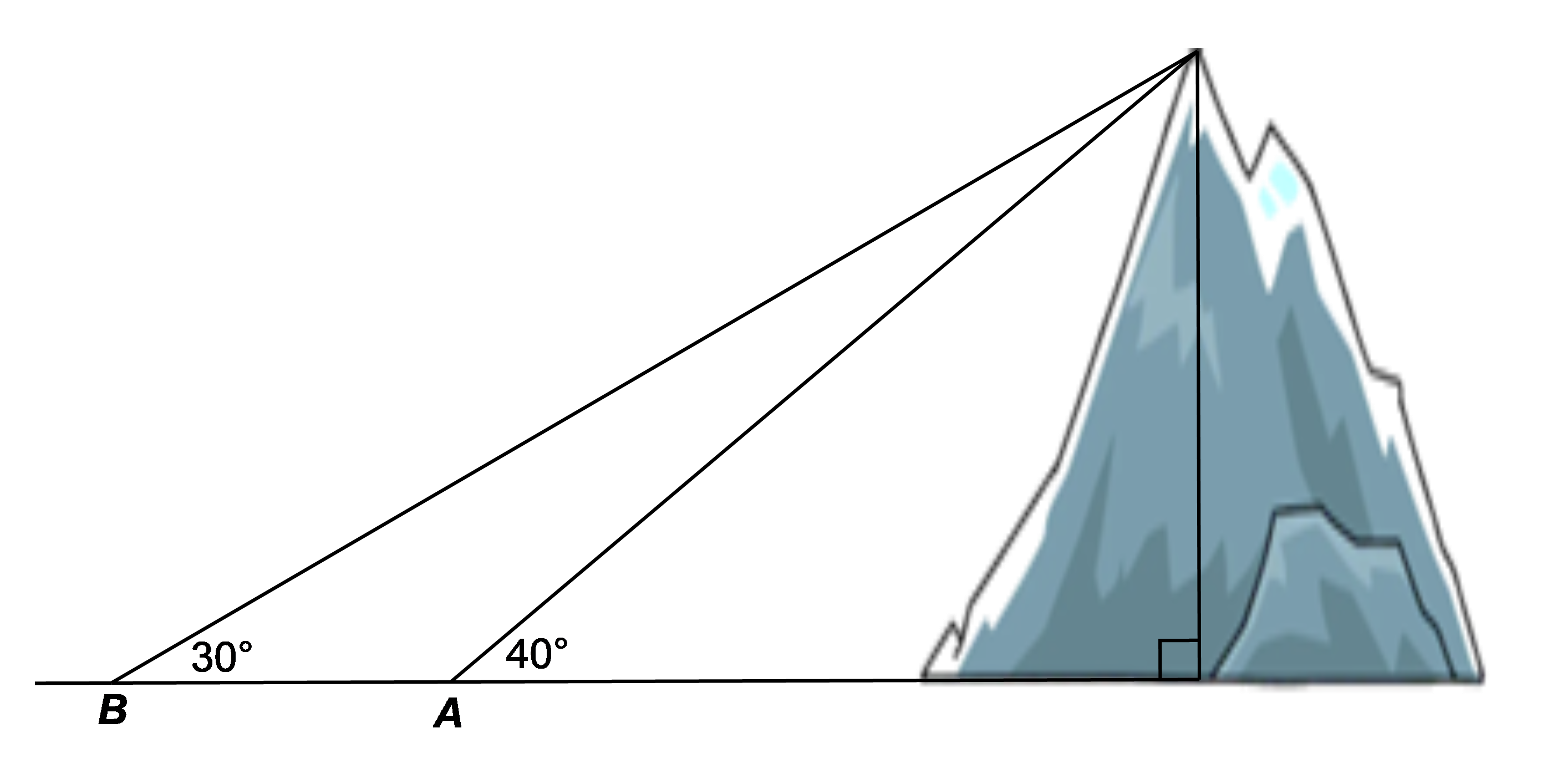
A. 1 110 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho tam giác đều \[MNP\] nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Phép quay ngược chiều \(240^\circ \) tâm \[O\] biến các điểm \(N,\,\,M,\,\,P\) thành các điểm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/12-1741763486.png)