Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh đất: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh \(x\left( {{\rm{\;m}}} \right)\); mảnh đất thứ hai có đạng hình chữ nhật với chiều dài \(x\left( {{\rm{\;m}}} \right)\) và chiều rộng \(y\left( {{\rm{\;m}}} \right)(x > y > 0)\) được minh hoạ ở Hinh 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là \(6,8{\rm{\;m}}\). Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1130000 đồng theo giá 50000 đồng/mét.
a) Viết hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số \(\left( {13;9,6} \right)\) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?
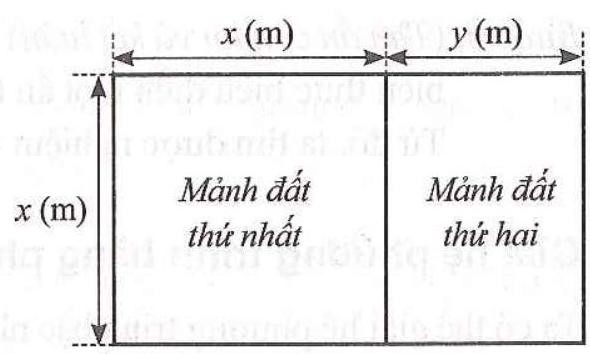
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh đất: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh \(x\left( {{\rm{\;m}}} \right)\); mảnh đất thứ hai có đạng hình chữ nhật với chiều dài \(x\left( {{\rm{\;m}}} \right)\) và chiều rộng \(y\left( {{\rm{\;m}}} \right)(x > y > 0)\) được minh hoạ ở Hinh 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là \(6,8{\rm{\;m}}\). Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1130000 đồng theo giá 50000 đồng/mét.
a) Viết hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng.
b) Cặp số \(\left( {13;9,6} \right)\) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Quảng cáo
Trả lời:
a) Do chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là \(6,8{\rm{\;m}}\) nên ta có phương trình: \(4x - 2\left( {x + y} \right) = 6,8\) hay \(x - y = 3,4\). Vậy hệ hai phương trình bậc nhất hai ẩn \(x,y\) biểu thị mối quan hệ giữa các đại lượng là:
\(\left\{ {\begin{array}{*{20}{l}}{x - y = 3,4}\\{x + y = 22,6}\end{array}} \right.\)
b) Học sinh tự làm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (triệu đồng), \(y\) (triệu đồng) lần lượt là số tiền mà cửa hàng đã vay từ ngân hàng A, \({\rm{B}}(x > 0,y > 0)\).
Theo giả thiết, ta có phương trình: \(x + y = 600\).
Mặt khác, ta có phương trình: \(8{\rm{\% }} \cdot x + 9{\rm{\% }} \cdot y = 51,5\) hay \(8x + 9y = 5150\).
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + y = 600}\\{8x + 9y = 5150}\end{array}} \right.\)
Từ phương trình (1), ta có: \(y = 600 - x\).
Thế \(y = 600 - x\) vào phương trình (2), ta được: \(8x + 9\left( {600 - x} \right) = 5150\)
Giải phương trình (3):
\(\begin{array}{*{20}{c}}{8x + 9\left( {600 - x} \right)\; = 5150\,\,\,\,}\\{8x + 5400 - 9x\; = 5150\,\,\,\,\,}\\{ - x + 5400\; = 5150\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{x\; = 250}\end{array}\)
Thay \(x = 250\) vào phương trình \(y = 600 - x\), ta có:
Do đó, phương trình đã cho có nghiệm duy nhất \(\left( {x;y} \right) = \left( {250;350} \right)\).
Vậy số tiền mà cửa hàng đã vay từ ngân hàng \({\rm{A}},{\rm{B}}\) lần lượt là 250 triệu đồng, 350 triệu đồng.
Lời giải
Gọi \(x\) (đồng) là giá niêm yết của một cái quạt điện, \(y\) (đồng) là giá niêm yết của một cái bàn ủi điện \(({\rm{x}} > 0,{\rm{y}} > 0)\).
Tổng số tiền theo giá niêm yết của hai sản phẩm là 900000 đồng, nên ta có phương trình: \(x + y = 900000\).(1)
Tổng số tiền của hai sản phẩm sau khi đã giảm giá là 780000 đồng, nên ta có phương trình: \(0,85x + 0,9y = 780000\)(2)
Từ (1) và \((2)\), ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 900000}\\{0,85x + 0,9y = 780000.}\end{array}} \right.\)
Giải hệ phương trình, ta được \(x = 600000,y = 300000\) (thoả mãn).
Vậy giá niêm yết của một cái quạt điện là 600000 đồng, giá niêm yết của một cái bàn ủi điện là 300000 đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.