2. Ôn vào 10
  3. Toán

Câu hỏi:

13/04/2025 98

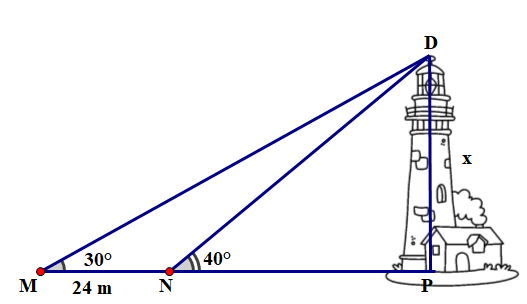
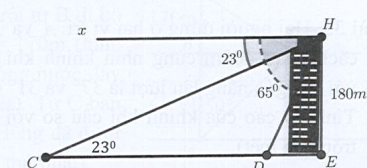
Một người đứng trên tòa nhà cao 180 m nhìn thấy hai chiếc xe ở vị trí C và D với góc hạ lần lượt là xHC^=23° và xHD^=65°. Tính khoảng cách CD của hai chiếc xe. (làm tròn đến chữ số thập phân thứ nhất)
Tính khoảng cách CD của hai chiếc xe. (làm tròn đến chữ số thập phân thứ nhất) (ảnh 1)

Xem lời giải

Câu hỏi trong đề: 52 bài tập Hệ thức lượng trong tam giác có lời giải !!

Bắt đầu thi Lưu câu hỏi

Quảng cáo

Trả lời:

verified
Giải bởi Vietjack
Vì Hx//CE⇒HCE^=xHC^=23°;HDE^=xHD^=65°
Xét △HED vuông tại \(E\), ta có: tanHDE=HEDE⇒tan65°=180DE⇒DE=180tan65°=83,9 m
Xét △HCE vuông tại \(E\), ta có: tanHCE=HECE⇒tan23°=180CE⇒CE=180tan23°=424,1
Ta có: \(CD = CE - DE = 424,1 - 83,9 = 340,2\;{\rm{m}}\).
Vậy khoảng cách của hai chiếc xe là \(340,2\;{\rm{m}}\).
Sách thầy cô Vietjack biên soạn:
Xem thêm »
  1. Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
  2. Sổ tay Lịch Sử 12 (chương trình mới) ( 18.000₫ )
  3. Sổ tay Địa Lí 12 (chương trình mới) ( 18.000₫ )
  4. Sổ tay Giáo dục Kinh tế & Pháp luật 12 (chương trình mới) ( 18.000₫ )

Bình luận


Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một người thợ thiết kế một tầng lửng cho căn phòng của anh ấy. Anh ấy đã hoàn thành bản vẽ và tính toán được chiếc thang phải dài 4,8 m đặt nghiêng sao cho tạo với mặt sàn một góc 58°. Hỏi độ cao của tầng lửng mà anh thiết kế là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất).

Hỏi độ cao của tầng lửng mà anh thiết kế là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ nhất). (ảnh 1)

Lời giải

Xét vuông tại \(B\), ta có:
sinACB=ABAC⇒sin58°=AB4,8⇒AB=4,8⋅sin58°≈4 m
Vậy độ cao của tầng lửng mà anh thiết kế là 4 m.

Câu 2

Một người cao 1,5 mét đứng cách nơi thả khinh khí cầu 250 mét nhìn thấy nó với góc nâng 38°như hình vẽ. Tính độ cao của khinh khí cầu so với mặt đất? (kết quả làm tròn đến mét).
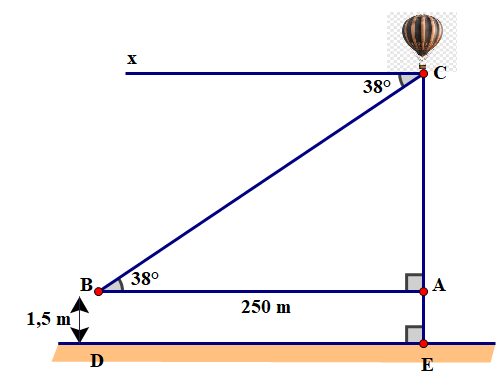
Tính độ cao của khinh khí cầu so với mặt đất? (kết quả làm tròn đến mét). (ảnh 1)

Lời giải

Tứ giác \(ABDE\) là hình chữ nhật nên \(AB = DE = 250\;{\rm{m}}\).
Xét △ABC vuông tại \(A\), ta có:
tanABC=ACAB⇒tan38°=AC250⇒AC=250⋅tan38°≈195 m
Ta có \(:{\rm{CE}} = {\rm{CA}} + {\rm{AE}} = 195 + 1,5 = 196,5\;{\rm{m}}\).
Vậy độ cao của khinh khí cầu so với mặt đất là 196,5m.

Câu 3

Tháp Eiffel là một công trình kiến trúc bằng thép nằm trên công viên Champ-de-Mars, cạnh sông Seinc, là biểu tượng của Thủ đô Paris nước Pháp. Công trình này do kỹ sư Gustave Eiffel và các đồng nghiệp của mình thiết kế, xây dựng từ năm 1887 đến năm 1889 nhân dịp Triển lãm thế giới năm 1889 và cũng là dịp kỷ niệm 100 năm Cách mạng Pháp. Hãy tính chiều cao của tháp Eiffel mà không cần lên đỉnh tháp khi biết góc tạo bởi tia nắng mặt trời với mặt đất là 62°C và bóng của tháp trên mặt đất là 175 m (làm tròn kết quả tới hàng đơn vị).

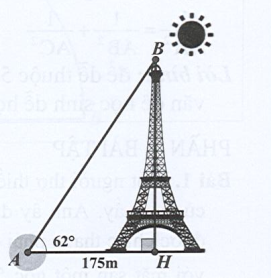
Hãy tính chiều cao của tháp Eiffel mà không cần lên đỉnh tháp khi biết góc tạo bởi tia nắng mặt trời với mặt đất là (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Để đo chiều cao của một ngọn hải đăng, người ta đặt giác kế tại 2 vị trí M và N sao cho các vị trí \({\rm{M}},{\rm{N}},{\rm{P}}\) cùng nằm trên một đường thẳng như hình vẽ. Kết quả thu được, vị trí M nhìn ngọn hải đăng dưới góc 30°, vị trí N nhìn ngọn hải đăng dưới góc 40°, khoảng cách giữa M và N là 24 m. Hỏi chiều cao \(DP\) của ngọn hải đăng là bao nhiêu mét? (làm tròn kết quả đến chữ số hàng đơn vị, học sinh không cần vẽ hình vào Câu làm).
Hỏi chiều cao DP của ngọn hải đăng là bao nhiêu mét? (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một cái cây bên bờ một con sông có bề rộng \({\rm{AC}} = 15\;{\rm{m}}\), từ một điểm C đối diện với cây ngay bờ bên kia người ta nhìn thấy ngọn cây với góc nâng ACB^=50°. Tính chiều cao AB của cây (kết quả làm tròn đến mét)

Tính chiều cao AB của cây (kết quả làm tròn đến mét) (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một máy bay cất cánh với vận tốc trung bình là \(300\;{\rm{km}}/{\rm{h}}\), sau 6 phút máy bay cách mặt đất so với phương thẳng đứng là \(15.000 \cdot 000\;{\rm{m}}\). Hỏi đường bay lên của máy bay tạo với phương nằm ngang so với mặt đất một góc bằng bao nhiêu độ và khoảng cách từ điểm cất cánh đến chân của đường vuông góc hạ từ máy bay xuống mặt đất lúc này là bao nhiêu? (làm tròn đến hàng đơn vị).
Hỏi đường bay lên của máy bay tạo với phương nằm ngang so với mặt đất một góc bằng bao nhiêu độ và khoảng cách từ điểm cất cánh đến chân của đường vuông góc hạ từ máy bay xuống mặt đất lúc này là bao nhiêu? (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một người đang ở vị trí \(B\) cách \(C\) là 400 m, quan sát hai lần một khinh khí cầu đang bay thẳng lên (như hình bên). Lần thứ nhất người đó nhìn thấy khinh khí cầu với góc nâng là 24°, lần thứ hai người đó nhìn thấy khinh khí cầu với góc nâng là 50°. Hỏi khinh khí cầu đã bay lên bao nhiêu mét giữa hai lần quan sát? (kết quả làm tròn đến hàng đơn vị).
Hỏi khinh khí cầu đã bay lên bao nhiêu mét giữa hai lần quan sát? (kết quả làm tròn đến hàng đơn vị). (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »
Hỏi bài tập
Vietjack official store
Đăng ký gói thi VIP

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

  • Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

🔥 Đề thi HOT:

  1. 1608 người thi tuần này

    123 bài tập Nón trụ cầu và hình khối có lời giải
  2. 1484 người thi tuần này

    Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
  3. 272 người thi tuần này

    50 bài tập Một số yếu tố xác suất có lời giải
  4. 219 người thi tuần này

    Đề thi tham khảo môn Toán vào 10 tỉnh Quảng Bình năm học 2025-2026
  5. 177 người thi tuần này

    Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_TP Hà Nội
  6. 162 người thi tuần này

    Đề thi minh họa (Dự thảo) TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đồng Nai
  7. 145 người thi tuần này

    Đề thi thử TS vào 10 (Lần 2 - Tháng 2) năm học 2025 - 2026_Môn Toán_THCS Hoằng Thanh_Tỉnh Thanh Hóa
  8. 129 người thi tuần này

    Đề thi tham khảo TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Bình Phước

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.

Đăng ký

Bạn đã có tài khoản?