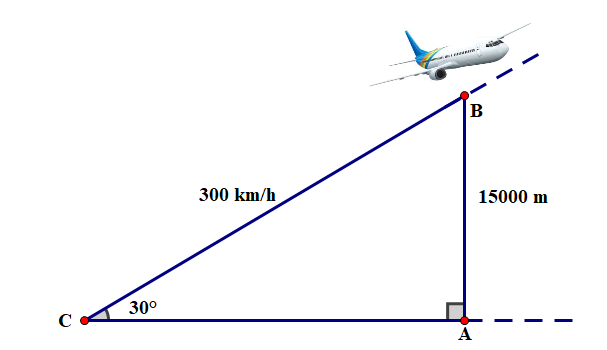
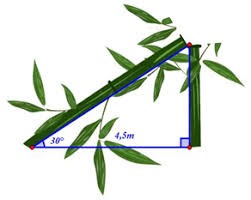
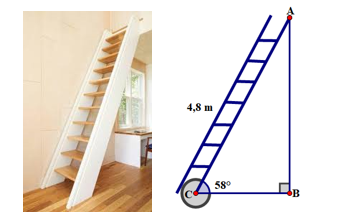
Để đo chiều cao của một bức tường Điệp dùng một quyển sách và ngắm sao cho hai cạnh bia của quyển sách hướng về vị trí cao nhất và vị trí thấp nhất của bức tường (xem hình bên). Biết rằng Điệp đứng cách tường \(1,5\;{\rm{m}}\) và vị trí mắt khi quan sát cách mặt đất là \(1,2\;{\rm{m}}\). Hỏi chiều cao của bức tường là bao nhiêu? (Kết quả làm tròn đến hàng đơn vị).

Câu hỏi trong đề: 52 bài tập Hệ thức lượng trong tam giác có lời giải !!
Quảng cáo
Trả lời:
H là hình chiếu của A lên BC.
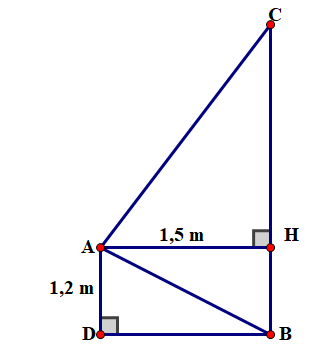
Tứ giác ADBH là hình chữ nhật nên \({\rm{BD}} = {\rm{AH}} = 1,5\;{\rm{m}}\);
\({\rm{BH}} = {\rm{AD}} = 1,2\;{\rm{m}}\)
\({\rm{A}}{{\rm{B}}^2} = {\rm{A}}{{\rm{D}}^2} + {\rm{B}}{{\rm{D}}^2} = 1,{2^2} + 1,{5^2} = 3,69 \Rightarrow {\rm{AB}} = \sqrt {3,69} = 1,92\;{\rm{m}}\)
Xét vuông tại A, đường cao AH, ta có: \({\rm{A}}{{\rm{B}}^2} = {\rm{BH}} \cdot {\rm{BC}} \Rightarrow {\rm{BC}} = \frac{{{\rm{A}}{{\rm{B}}^2}}}{{{\rm{BH}}}} = \frac{{3,69}}{{1,2}} \approx 3\;{\rm{m}}\)
Vậy chiều cao của bức tường là 3 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
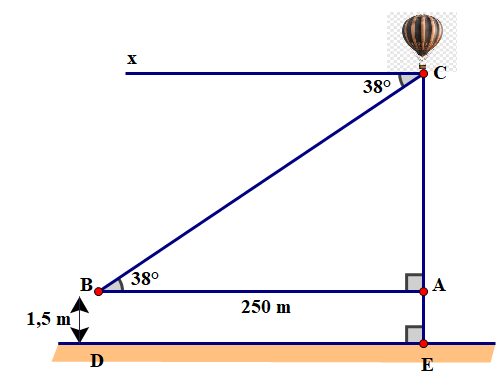
Xét vuông tại \(A\), ta có:
Ta có \(:{\rm{CE}} = {\rm{CA}} + {\rm{AE}} = 195 + 1,5 = 196,5\;{\rm{m}}\).
Vậy độ cao của khinh khí cầu so với mặt đất là 196,5m.
Lời giải
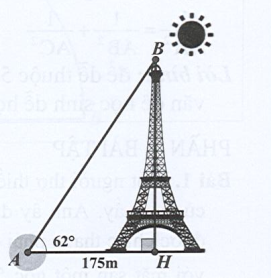
Vậy chiều cao của tháp Eiffel là 329 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.