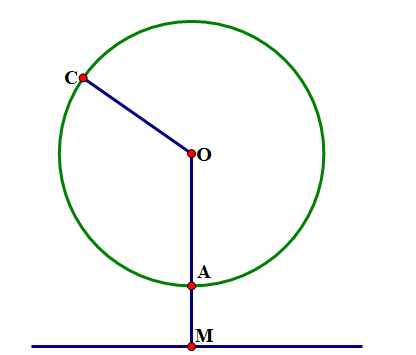
Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính \(1,2\;{\rm{m}}\). Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có 1 kích thước là \(1,2\;{\rm{m}}\) như hình vẽ bên. Hỏi kích thước kia của hình chữ nhật phải là bao nhiêu để diện tích mặt bàn tăng gấp ba sau khi nới? (làm tròn đến hàng phần chục, đơn vị \({\rm{cm}},\pi = 3,14\) ).
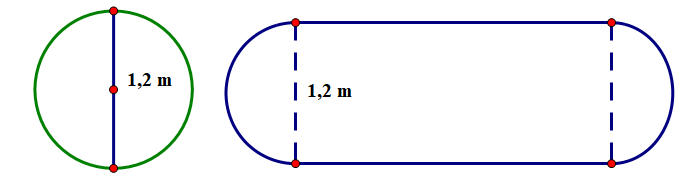
Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính \(1,2\;{\rm{m}}\). Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có 1 kích thước là \(1,2\;{\rm{m}}\) như hình vẽ bên. Hỏi kích thước kia của hình chữ nhật phải là bao nhiêu để diện tích mặt bàn tăng gấp ba sau khi nới? (làm tròn đến hàng phần chục, đơn vị \({\rm{cm}},\pi = 3,14\) ).
Câu hỏi trong đề: 62 bài tập Đa giác nội tiếp và đa giác đều có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(x(\;{\rm{m}})\) là kích thước kia của hình chữ nhật \((x > 0)\).
Diện tích mặt bàn hình tròn là \(\pi \cdot {\left( {\frac{{1,2}}{2}} \right)^2} = 0,36\pi \left( {{{\rm{m}}^2}} \right)\).
Diện tích mặt bàn sau khi nới là \(0,36\pi + 1,2x\left( {\;{{\rm{m}}^2}} \right)\).
Ta có phương trình: \(0,36\pi + 1,2x = 3.0,36\pi \Leftrightarrow 1,2x = 0,72\pi \Leftrightarrow x = 0,6\pi \approx 1,884\;{\rm{m}} = 188,4\;{\rm{cm}}\)
Vậy kích thước kia của hình chữ nhật là \(188,4\;{\rm{cm}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
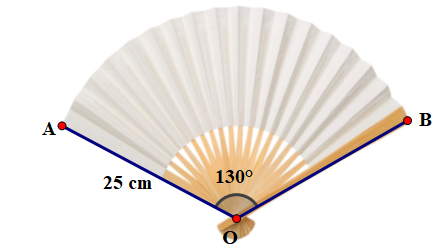
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
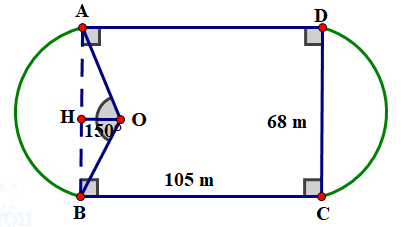
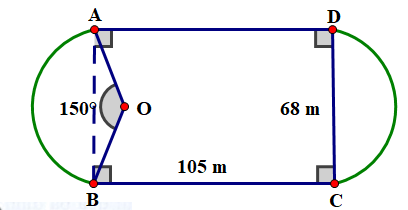
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có:
Xét vuông tại \(H\), ta có:
Độ dài cung AB là:
Vậy chu vi sân khoảng 394,3 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập