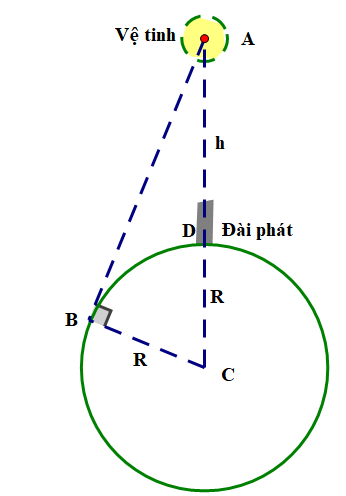
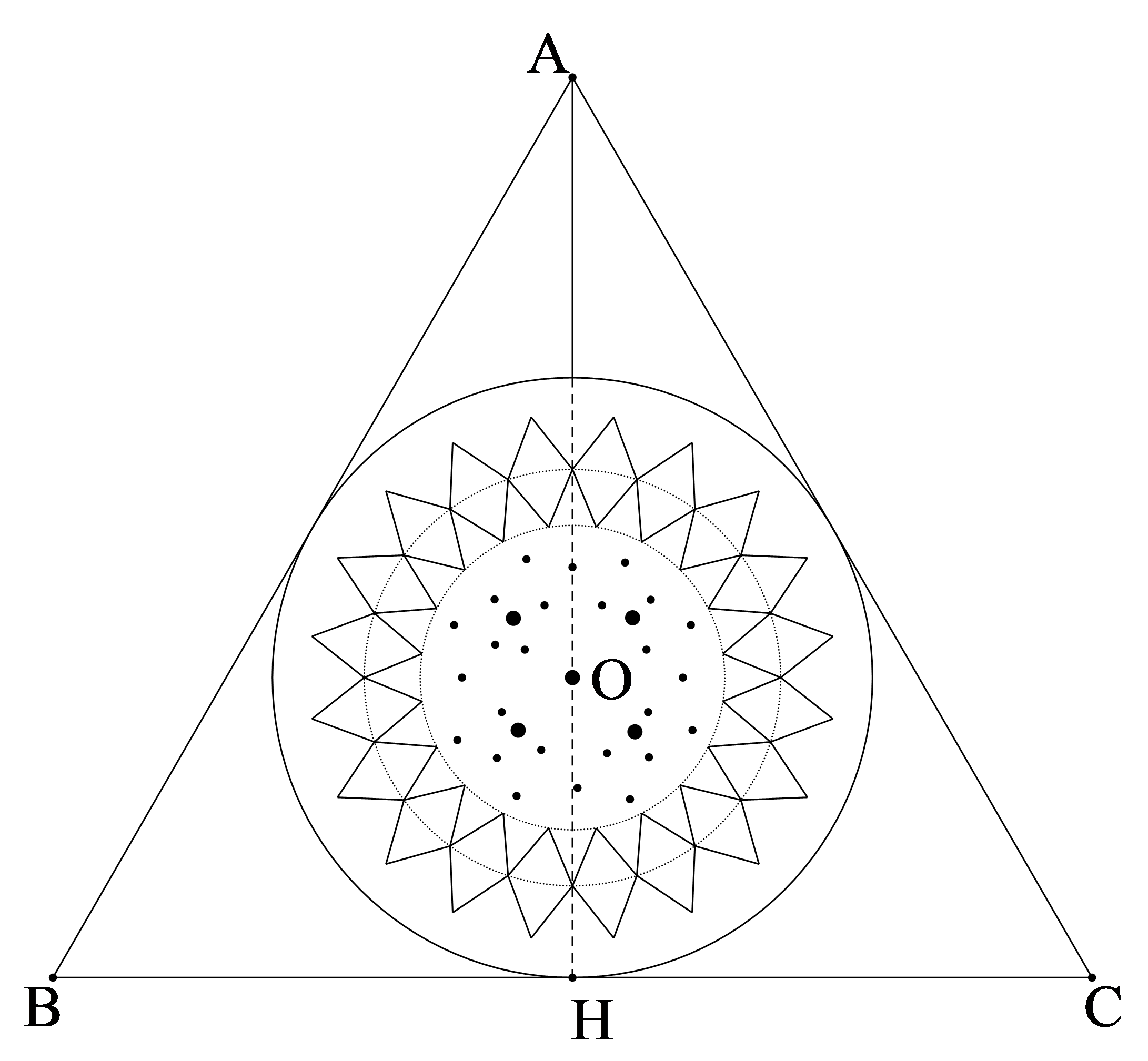Một vệ tinh thông tin (vệ tinh địa tĩnh) chuyển động trên quỹ đạo tròn ngay phía trên xích đạo của Trái Đất, quay cùng hướng và cùng chu kì tự quay của Trái Đất ở độ cao 36600 km so với đài phát trên mặt đất. Đài phát nằm trên đường thẳng nối vệ tinh và tâm Trái Đất. Ta xem Trái Đất là một hình cầu có bán kính 6400 km . Vệ tinh nhận sóng truyền hình từ đài phát rồi phát lại tức thời tín hiệu đó về Trái Đất. Tốc độ truyền sóng là \(3 \cdot {10^8}\;{\rm{m}}/{\rm{s}}\). Tính khoảng thời gian lón nhất mà sóng truyền hình đi từ đài phát đến một điểm trên mặt Trái Đất, với hình minh hoạ bên dưới. (kết quả làm tròn ba số thập phân).
Câu hỏi trong đề: 62 bài tập Đa giác nội tiếp và đa giác đều có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khoảng thời gian lớn nhất mà sóng truyền hình đi từ đài phát đến một điểm trên mặt Trái Đất tương ứng với thời gian sóng truyền từ điểm D đến A sau đó từ A về B .
Xét vuông tại \(B\), ta có: \(A{C^2} = A{B^2} + B{C^2}\) (định lý Pythagore).
Nên \(AB = \sqrt {{\rm{A}}{{\rm{C}}^2} - {\rm{B}}{{\rm{C}}^2}} = \sqrt {{{(6400 + 36600)}^2} - {{6400}^2}} = \sqrt {1808040000} (\;{\rm{km}})\) \( = \sqrt {1808040000} \cdot {10^3}(\;{\rm{m}})\)
Thời gian sóng truyền từ \(D\) đến \(A\) là \(\frac{{36600000}}{{3 \cdot {{10}^8}}} = \frac{{61}}{{500}}\) (giây).
Thời gian sóng truyền từ A đến B là \(\frac{{\sqrt {1808040000} \cdot {{10}^3}}}{{3 \cdot {{10}^8}}}\) (giây).
Khoảng thời gian lớn nhất mà sóng truyền hình đi từ đài phát đến một điểm trên mặt Trái Đất là \(\frac{{61}}{{500}} + \frac{{\sqrt {1808040000} \cdot {{10}^3}}}{{3 \cdot {{10}^8}}} \approx 0,264\) (giây).
Vậy khoảng thời gian lớn nhất mà sóng truyền hình đi từ đài phát đến một điểm trên mặt Trái Đất là khoảng 0,264 giây.
Xét vuông tại \(B\), ta có: \(A{C^2} = A{B^2} + B{C^2}\) (định lý Pythagore).
Nên \(AB = \sqrt {{\rm{A}}{{\rm{C}}^2} - {\rm{B}}{{\rm{C}}^2}} = \sqrt {{{(6400 + 36600)}^2} - {{6400}^2}} = \sqrt {1808040000} (\;{\rm{km}})\) \( = \sqrt {1808040000} \cdot {10^3}(\;{\rm{m}})\)
Thời gian sóng truyền từ \(D\) đến \(A\) là \(\frac{{36600000}}{{3 \cdot {{10}^8}}} = \frac{{61}}{{500}}\) (giây).
Thời gian sóng truyền từ A đến B là \(\frac{{\sqrt {1808040000} \cdot {{10}^3}}}{{3 \cdot {{10}^8}}}\) (giây).
Khoảng thời gian lớn nhất mà sóng truyền hình đi từ đài phát đến một điểm trên mặt Trái Đất là \(\frac{{61}}{{500}} + \frac{{\sqrt {1808040000} \cdot {{10}^3}}}{{3 \cdot {{10}^8}}} \approx 0,264\) (giây).
Vậy khoảng thời gian lớn nhất mà sóng truyền hình đi từ đài phát đến một điểm trên mặt Trái Đất là khoảng 0,264 giây.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
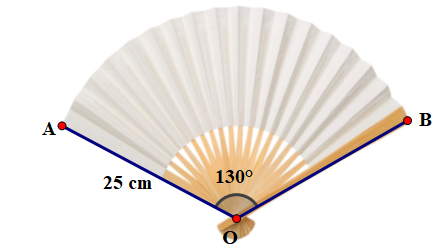
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Lời giải
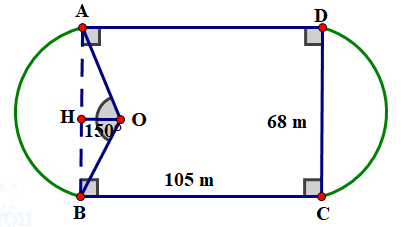
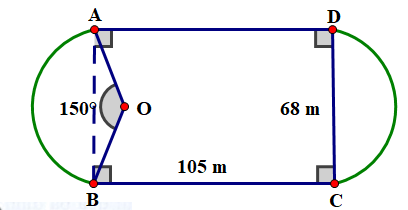
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có:
Xét vuông tại \(H\), ta có:
Độ dài cung AB là:
Vậy chu vi sân khoảng 394,3 m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập