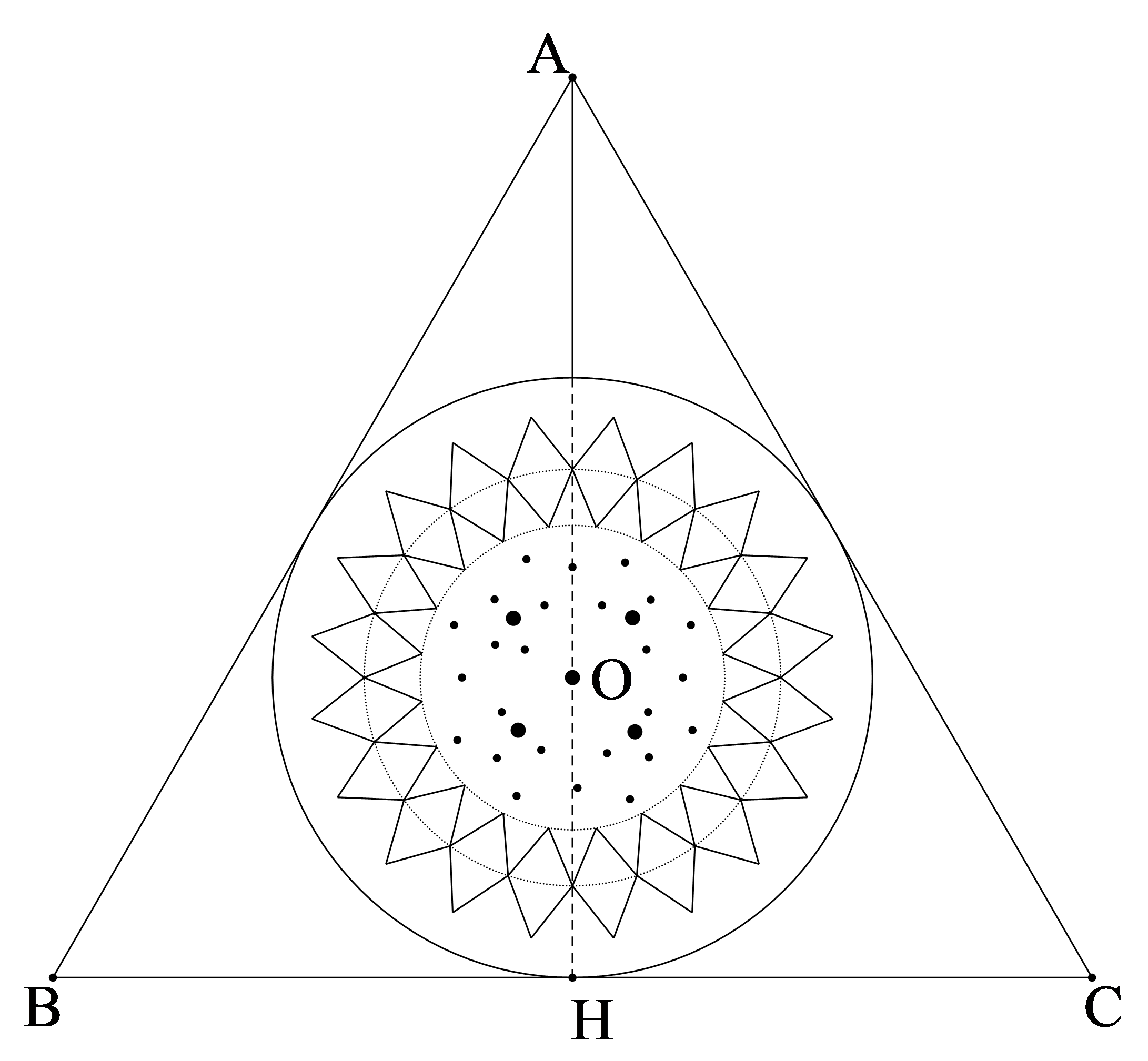Mộttấm poster hình tam giác đều mỗi cạnh \[5\]\[dm\]. Ba cung tròn \[DE,{\rm{ }}EF,{\rm{ }}FD\] thuộc \[3\] đường tròn bán kính \[2,5\]\[dm\] có tâm lần lượt là \[3\] điểm \[A,{\rm{ }}B,{\rm{ }}C\]. Tính diện tích phần còn lại (không tô màu) của tam giác (cho biết \[\mu = 3,14\] và kết quả làm đúng đơn vị \[d{m^2}\]).
Câu hỏi trong đề: 62 bài tập Đa giác nội tiếp và đa giác đều có lời giải !!
Quảng cáo
Trả lời:
![Tính diện tích phần còn lại (không tô màu) của tam giác (cho biết \[\mu = 3,14\] và kết quả làm đúng đơn vị \[d{m^2}\]). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/04/37-1744537767.png)
\[S\] (\[3\]hình quạt tròn) là \[\left( {3,14.2,{5^2}} \right):2 = 9,8125\]\[\left( {d{m^2}} \right)\]
\[S\] (tam giác đều cạnh \[5\]\[dm\]) là \[\left( {{5^2}.\sqrt 3 } \right):4 \approx 10,8125\]\[\left( {d{m^2}} \right)\]
\[S\]phần còn lại là: \[10,8125 - 9,8125 = 1\]\[\left( {d{m^2}} \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
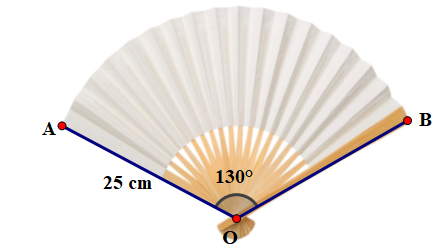
a) Diện tích hình quạt là: \({\rm{S}} = \frac{{\pi {{\rm{R}}^2}{\rm{n}}}}{{360}} = \frac{{\pi \cdot {{25}^2} \cdot 130}}{{360}} \approx 709\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
b) Diện tích giấy làm 100 cây quạt là: \(709 \cdot 2 \cdot 100 = 141800\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Lời giải
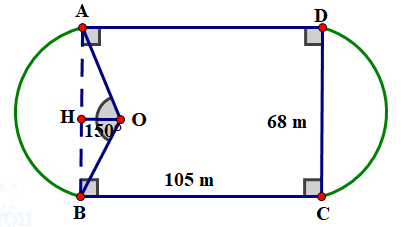
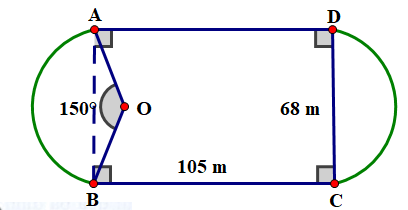
Kẻ \({\rm{OH}} \bot {\rm{AB}}\) tại \(H\), ta có:
Xét vuông tại \(H\), ta có:
Độ dài cung AB là:
Vậy chu vi sân khoảng 394,3 m.
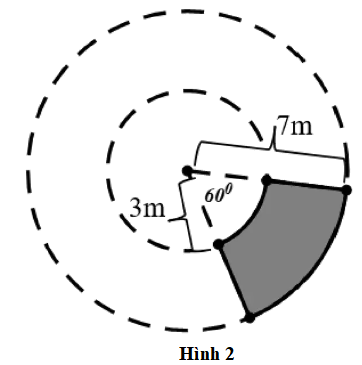
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.