Cho tam giác vuông có góc \(\alpha \) là góc nhọn. Khẳng định sai là
Câu hỏi trong đề: 63 bài tập Tỉ số lượng giác và ứng dụng có lời giải !!
Quảng cáo
Trả lời:
Theo định nghĩa tỉ số lượng giác trong tam giác vuông.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
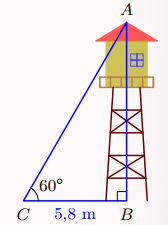
Câu 1
Lời giải
Xét \[\Delta ABC\] vuông tại \[B\]
Áp dụng tỉ số lượng giác trong tam giác trong tam giác vuông ABC ta có
\[\tan C = \frac{{AB}}{{CB}}\], suy ra \[AB = BC \cdot \tan C\] hay \[AB = 5,8 \cdot \tan 60^\circ = 5,8 \cdot \sqrt 3 \approx 10,05\] (m)
Vậy chiều cao của tháp canh gần bằng \[10,05\] mét.
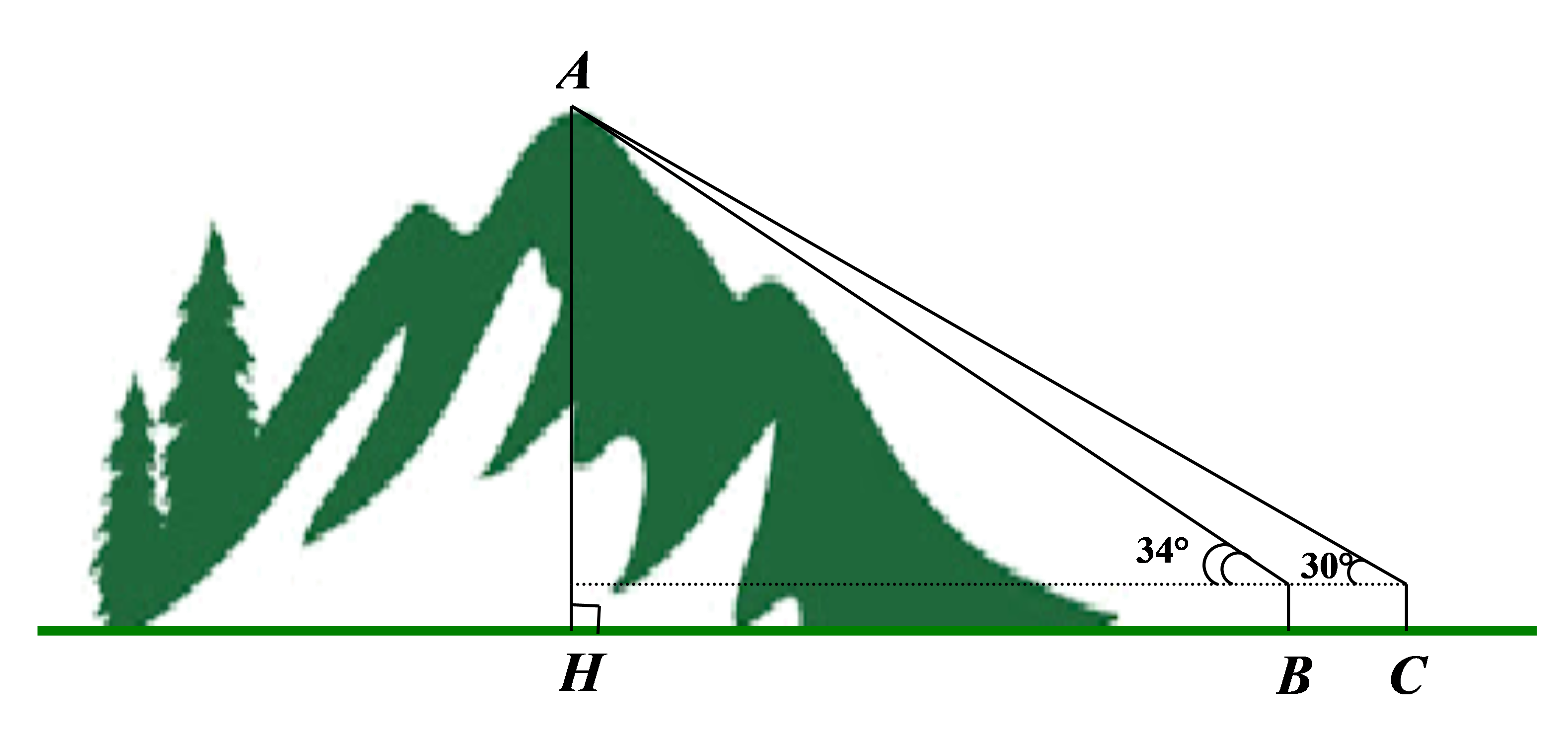
Câu 2
Lời giải
Do Mặt đất là phương ngang nên \[\widehat {BCA} = 30^\circ \] và \[\widehat {BDA} = 60^\circ \].
Gọi \[x\](m/phút) là vận tốc xe máy, điều kiện \[x > 0\].
Vì xe máy đi từ \[C\] đến \[D\] trong \[6\] phút nên \[CD = 6x\,\,\left( {\rm{m}} \right)\]
Xét \[\Delta ABC\] vuông tại \[A\], áp dụng hệ thức giữa cạnh và góc nhọn trong tam giác ta có:
\[AC = AB.\,\cot \widehat {BCA} = AB.\,\cot {30^{\rm{o}}} = AB.\tan {60^{\rm{o}}} = \sqrt 3 AB\] (do \[\cot {30^{\rm{o}}} = \tan {60^{\rm{o}}}\]) \[\left( 1 \right)\]
Xét \[\Delta ABD\] vuông tại \[A\], áp dụng hệ thức giữa cạnh và góc nhọn trong tam giác ta có:
\[AD = AB.\,\cot \widehat {BDA} = AB.\,\cot {60^{\rm{o}}} = AB.\tan {30^{\rm{o}}} = \frac{{\sqrt 3 AB}}{3}\] (do \[\cot {60^{\rm{o}}} = \tan {30^{\rm{o}}}\]) \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[AC - AD = AB\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right) \Rightarrow CD = \frac{{2\sqrt 3 }}{3}AB\].
Xét tỉ số \[\frac{{AD}}{{CD}} = \frac{{\sqrt 3 AB}}{3}:\frac{{2\sqrt 3 }}{3}AB = \frac{1}{2} \Rightarrow AD = \frac{1}{2}CD = \frac{1}{2}.6x = 3x\,\,\left( {\rm{m}} \right)\]
Vậy thời gian để xe máy chạy từ \[D\] đến tòa nhà là \[\frac{{3x}}{x} = 3\] (phút).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.