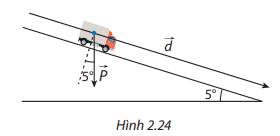
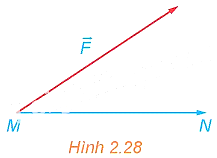
Như đã biết, nếu có một lực \(\vec F\) tác động vào một vật tại điểm \(M\) và làm cho vật đó di chuyển một quãng đường \({\rm{MN}}\) thì công \({\rm{A}}\) sinh ra được tính theo công thức \(A = \vec F \cdot \overrightarrow {MN} \), trong đó lực \({\rm{F}}\) có độ lớn tính bằng Newton, quãng đường \(MN\) tính bằng mét và công \(A\) tính bằng Jun (H.2.28). Do đó, nếu dùng một lực \(\vec F\) có độ lớn không đổi để lâm một vật di chuyển một quãng đường không đối thì công sinh ra sê lớn nhất khi lực tác đônng cưng hướng với chuyển động của vật. Hây giải thích vì sao. Kết quả trên có thể được áp dụng như thể nảo khi kêo (hoặc đầy) các vật nặng?
Câu hỏi trong đề: Các dạng bài tập Vectơ trong không gian lớp 12 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(A = \vec F \cdot \overrightarrow {MN} = \left| {\vec F\left| \cdot \right|\overrightarrow {MN} } \right| \cdot {\rm{cos}}\left( {\vec F,\overrightarrow {MN} } \right)\)
vì lực \(\vec F\) có độ lớn không đổi và vật di chuyển một quãng đường không đổi nên \(A\) lớn nhất khi \({\rm{cos}}\left( {\vec F,\overrightarrow {MN} } \right)\) lớn nhất. Do đó, \({\rm{cos}}\left( {\vec F,\overrightarrow {MN} } \right) = 1 \Leftrightarrow \left( {\vec F,\overrightarrow {MN} } \right) = {0^0}\). Khi đó, lực tác động cùng hướng với chuyển động của vật. Vậy công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật.
Khi kéo (hoặc đẩy) các vật nặng, ta nên kéo (hoặc đẩy) cùng cùng hướng với chuyển động của vật.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
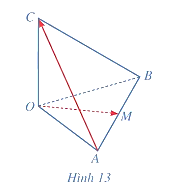
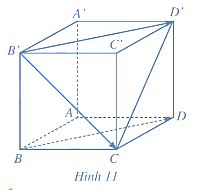
Đặt \(\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b,\overrightarrow {OC} = \vec c\).
Khi đó, \(\left| {\vec a\left| = \right|\vec b\left| = \right|\vec c} \right| = 1\) và \(\vec a \cdot \vec b = \vec a \cdot \vec c = \vec b \cdot \vec c = 0\).
Ta có: \({\rm{cos}}\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {OM} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {OM} \left| \cdot \right|\overrightarrow {AC} } \right|}}\).
Mặt khác, do \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {\vec a + \vec b} \right)\) và \(\overrightarrow {AC} = \overrightarrow {OC} - \overrightarrow {OA} = \vec c - \vec a\) nên \(\overrightarrow {OM} \cdot \overrightarrow {AC} = \frac{1}{2}\left( {\vec a + \vec b} \right) \cdot \left( {\vec c - \vec a} \right)\) \( = \frac{1}{2}\left( {\vec a \cdot \vec c - {{\vec a}^2} + \vec b \cdot \vec c - \vec b \cdot \vec a} \right) = - \frac{1}{2}.\)
Ta lại có: \(\left| {\overrightarrow {OM} \left| { = OM = \frac{{\sqrt 2 }}{2};} \right|\overrightarrow {AC} } \right| = AC = \sqrt 2 \).
Do đó, \({\rm{cos}}\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = \frac{{\frac{{\overrightarrow {OM} }}{{\overrightarrow {AC} }} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {OM} \left| \cdot \right|\overrightarrow {AC} } \right|}} = \frac{{\frac{{ - 1}}{2}}}{{\frac{{\sqrt 2 }}{2} \cdot \sqrt 2 }} = \frac{{ - 1}}{2}\).
Vậy \(\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = {120^ \circ }\).
Lời giải
Trả lời: \(n = - 0,5\)
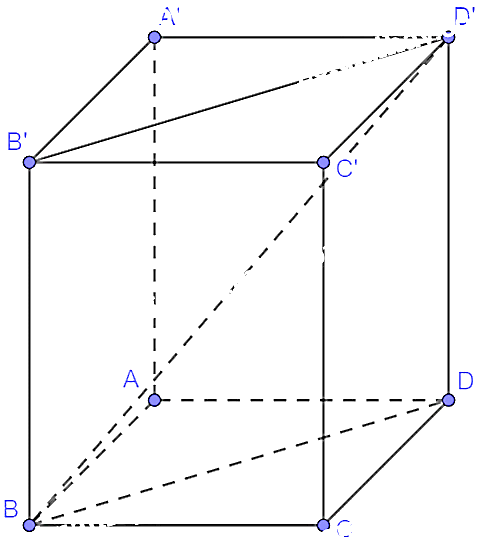
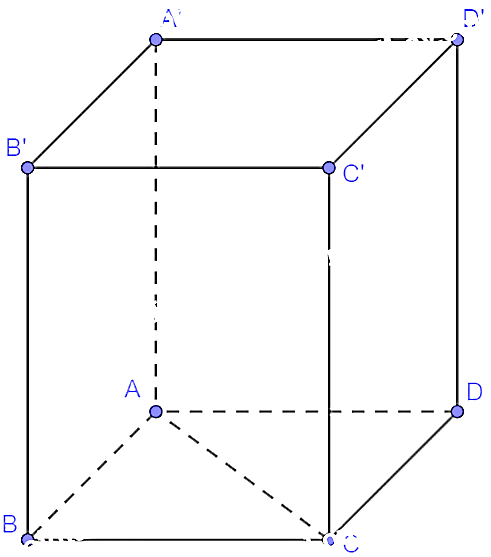
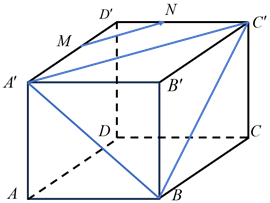
Vì \(MN//{A^\prime }{C^\prime }\) nên .
Ta có: \(MN = \frac{{a\sqrt 2 }}{2},{C^\prime }B = a\sqrt 2 \). Suy ra
Vậy \(n = - 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập