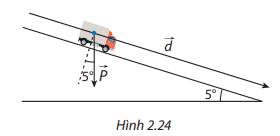
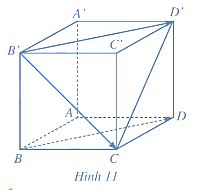
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({100^ \circ }\) và có độ lớn lần lượt là \(25{\rm{\;N}}\) và \(12{\rm{\;N}}\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(4{\rm{\;N}}\). Tính độ lớn của hợp lực của ba lực trên.

Quảng cáo
Trả lời:
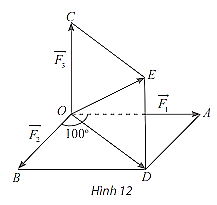
Gọi \({\vec F_1},{\vec F_2},{\vec F_3}\) là ba lực tác động vào vật đặt tại điểm \(O\) lần lượt có độ lớn là \(25{\rm{\;N}},12{\rm{\;N}},4{\rm{\;N}}\).
Vẽ \(\overrightarrow {OA} = {\vec F_1},\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = {\vec F_3}\).
Dựng hình bình hành \(OADB\) và hình bình hành \(ODEC\).
Hợp lực tác động vào vật là
\(\vec F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \)
Áp dụng định lí côsin trong tam giác \(OBD\), ta có
\(O{D^2} = B{D^2} + O{B^2} - 2 \cdot BD \cdot OB \cdot {\rm{cos}}\widehat {OBD} = O{A^2} + O{B^2} + 2 \cdot OA \cdot OB \cdot {\rm{cos}}{100^ \circ }\).
Vì \(OC \bot \left( {OADB} \right)\) nên \(OC \bot OD\), suy ra \(ODEC\) là hình chữ nhật.
Do đó tam giác \(ODE\) vuông tại \(D\).
Ta có \(O{E^2} = O{C^2} + O{D^2} = O{C^2} + O{A^2} + O{B^2} + 2 \cdot OA \cdot OB \cdot {\rm{cos}}{100^ \circ }\).
Suy ra \(OE = \sqrt {O{C^2} + O{A^2} + O{B^2} + 2 \cdot OA \cdot OB \cdot {\rm{cos}}{{100}^ \circ }} \)
\( = \sqrt {{4^2} + {{25}^2} + {{12}^2} + 2 \cdot 25 \cdot 12 \cdot {\rm{cos}}{{100}^ \circ }} \approx 26,092.\)
Vậy độ lớn của hợp lực là \(F = OE \approx 26{\rm{\;N}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đặt \(\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b,\overrightarrow {OC} = \vec c\).
Khi đó, \(\left| {\vec a\left| = \right|\vec b\left| = \right|\vec c} \right| = 1\) và \(\vec a \cdot \vec b = \vec a \cdot \vec c = \vec b \cdot \vec c = 0\).
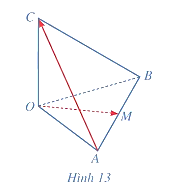
Ta có: \({\rm{cos}}\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {OM} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {OM} \left| \cdot \right|\overrightarrow {AC} } \right|}}\).
Mặt khác, do \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {\vec a + \vec b} \right)\) và \(\overrightarrow {AC} = \overrightarrow {OC} - \overrightarrow {OA} = \vec c - \vec a\) nên \(\overrightarrow {OM} \cdot \overrightarrow {AC} = \frac{1}{2}\left( {\vec a + \vec b} \right) \cdot \left( {\vec c - \vec a} \right)\) \( = \frac{1}{2}\left( {\vec a \cdot \vec c - {{\vec a}^2} + \vec b \cdot \vec c - \vec b \cdot \vec a} \right) = - \frac{1}{2}.\)
Ta lại có: \(\left| {\overrightarrow {OM} \left| { = OM = \frac{{\sqrt 2 }}{2};} \right|\overrightarrow {AC} } \right| = AC = \sqrt 2 \).
Do đó, \({\rm{cos}}\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = \frac{{\frac{{\overrightarrow {OM} }}{{\overrightarrow {AC} }} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {OM} \left| \cdot \right|\overrightarrow {AC} } \right|}} = \frac{{\frac{{ - 1}}{2}}}{{\frac{{\sqrt 2 }}{2} \cdot \sqrt 2 }} = \frac{{ - 1}}{2}\).
Vậy \(\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = {120^ \circ }\).
Lời giải
Trả lời: \(n = - 0,5\)
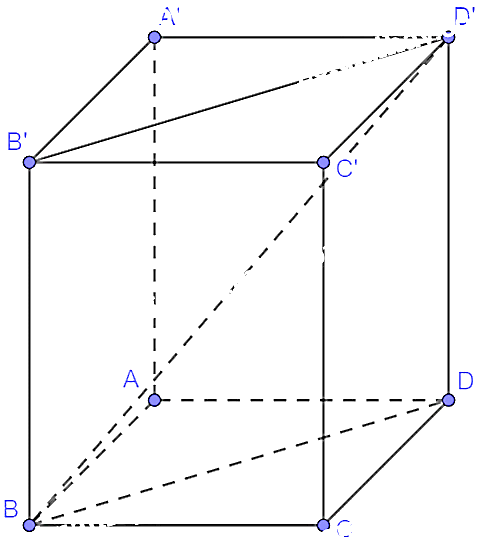
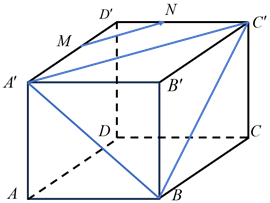
Vì \(MN//{A^\prime }{C^\prime }\) nên .
Ta có: \(MN = \frac{{a\sqrt 2 }}{2},{C^\prime }B = a\sqrt 2 \). Suy ra
Vậy \(n = - 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.