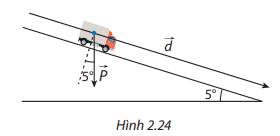
Theo định luật II Newton (Vật lí 10 - Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 60): Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật:

\(\vec F = m\vec a\)
trong đó \(\vec a\) là vectơ gia tốc \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right),\vec F\) là vectơ lực (N)
Hình 20 tác dụng lên vật, \(m\left( {{\rm{\;kg}}} \right)\) là khối lượng của vật.
Muốn truyền cho quả bóng có khối lượng \(0,5{\rm{\;kg}}\) một gia tốc \(50{\rm{\;m}}/{{\rm{s}}^2}\) thì cần một lực đá có độ lớn là bao nhiêu?

\(\vec F = m\vec a\)
trong đó \(\vec a\) là vectơ gia tốc \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right),\vec F\) là vectơ lực (N)
Hình 20 tác dụng lên vật, \(m\left( {{\rm{\;kg}}} \right)\) là khối lượng của vật.
Muốn truyền cho quả bóng có khối lượng \(0,5{\rm{\;kg}}\) một gia tốc \(50{\rm{\;m}}/{{\rm{s}}^2}\) thì cần một lực đá có độ lớn là bao nhiêu?
Quảng cáo
Trả lời:
Ta có \(\vec F = m\vec a\), suy ra \(\left| {\vec F\left| { = m} \right|\vec a} \right| = 0,5.50 = 25\left( {{\rm{\;N}}} \right)\).
Vậy muốn truyền cho quả bóng khối lượng \(0,5{\rm{\;kg}}\) một gia tốc \(50{\rm{\;m}}/{{\rm{s}}^2}\) thì cần một lực đá có độ lớn là \(25{\rm{\;N}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
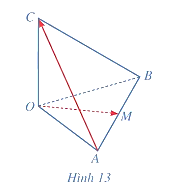
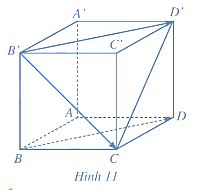
Đặt \(\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b,\overrightarrow {OC} = \vec c\).
Khi đó, \(\left| {\vec a\left| = \right|\vec b\left| = \right|\vec c} \right| = 1\) và \(\vec a \cdot \vec b = \vec a \cdot \vec c = \vec b \cdot \vec c = 0\).
Ta có: \({\rm{cos}}\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = \frac{{\overrightarrow {OM} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {OM} \left| \cdot \right|\overrightarrow {AC} } \right|}}\).
Mặt khác, do \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {\vec a + \vec b} \right)\) và \(\overrightarrow {AC} = \overrightarrow {OC} - \overrightarrow {OA} = \vec c - \vec a\) nên \(\overrightarrow {OM} \cdot \overrightarrow {AC} = \frac{1}{2}\left( {\vec a + \vec b} \right) \cdot \left( {\vec c - \vec a} \right)\) \( = \frac{1}{2}\left( {\vec a \cdot \vec c - {{\vec a}^2} + \vec b \cdot \vec c - \vec b \cdot \vec a} \right) = - \frac{1}{2}.\)
Ta lại có: \(\left| {\overrightarrow {OM} \left| { = OM = \frac{{\sqrt 2 }}{2};} \right|\overrightarrow {AC} } \right| = AC = \sqrt 2 \).
Do đó, \({\rm{cos}}\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = \frac{{\frac{{\overrightarrow {OM} }}{{\overrightarrow {AC} }} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {OM} \left| \cdot \right|\overrightarrow {AC} } \right|}} = \frac{{\frac{{ - 1}}{2}}}{{\frac{{\sqrt 2 }}{2} \cdot \sqrt 2 }} = \frac{{ - 1}}{2}\).
Vậy \(\left( {\overrightarrow {OM} ,\overrightarrow {AC} } \right) = {120^ \circ }\).
Lời giải
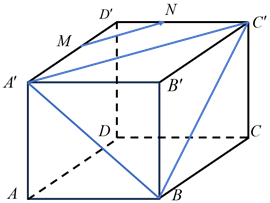
Trả lời: \(n = - 0,5\)
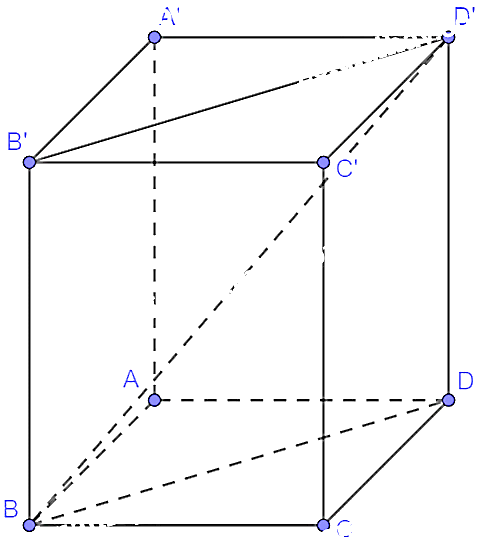
Vì \(MN//{A^\prime }{C^\prime }\) nên .
Ta có: \(MN = \frac{{a\sqrt 2 }}{2},{C^\prime }B = a\sqrt 2 \). Suy ra
Vậy \(n = - 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.