Các mệnh đề sau đúng hay sai?

Giá trị nhỏ nhất của hàm số \(f(x) = {x^3} + 3{x^2} - 9x - 7\) trên đoạn \([ - 4;0]\) bằng\[ - 7\]

Xét hàm số \(y = {x^3} - 3{x^2} - 9x + 35\) liên tục trên đoạn \(\left[ { - 4;4} \right]\), ta có:\(y' = 3{x^2} - 6x - 9\).

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1 \in \left[ { - 4;4} \right]\\x = 3 \in \left[ { - 4;4} \right]\end{array} \right.\).

Xét: \(y( - 4) =  - 41;\,\,y( - 1) = 40;\,\,y(3) = 8;\,\,y(4) = 15\). Vậy . Chọn S

Hàm số liên tục trên đoạn \(\left[ {0\,;\,5} \right]\)

Ta có: \(f'\left( x \right) = 8{x^3} - 8x\), \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x =  - 1\end{array} \right.\)

Xét hàm số trên đoạn \(\left[ {0\,;\,5} \right]\) có: \(f\left( 0 \right) = 1\); \(f\left( 1 \right) =  - 1\); \(f\left( 5 \right) = 1151\).

Vậy \(\mathop {\min }\limits_{x \in \left[ {0\,;\,5} \right]} f\left( x \right) =  - 1\). Chọn Đ

Hàm số liên tục trên đoạn \(\left[ {1;3} \right]\).

Ta có: \(y' = 1 + \frac{1}{{{x^2}}} > 0\,\forall x \ne 0\)\( \Rightarrow \) hàm số đồng biến trên đoạn \(\left[ {1;3} \right]\).

Vậy \(\mathop {Min}\limits_{\left[ {1;3} \right]} y = y\left( 1 \right) = 0\). Chọn Đ

Ta có

Khi đó  Chọn Đ

Ta có:\[y' = 3{x^2} - 6x - 9\].

Cho\[y' = 0 \Rightarrow 3{x^2} - 6x - 9 = 0 \Rightarrow \left[ \begin{array}{l}x =  - 1\\x = 3\end{array} \right.\]

Mặt kháC. \[y\left( { - 2} \right) =  - 4;y\left( { - 1} \right) = 3;y\left( 3 \right) =  - 29;y\left( 4 \right) =  - 22\].

Vậy \[\mathop {Min}\limits_{\left[ { - 2;4} \right]}  =  - 29\]. Chọn Đ

Ta có: \(y' = 3{x^2} - 12\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 2\end{array} \right.\)..

Vì \(f\)liên tục trên đoạn \(\left[ { - 2;3} \right]\)mà \(f\left( { - 2} \right) = 17;\,f\left( 2 \right) =  - 15;\,f\left( 3 \right) =  - 8\).

Nên giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là \(17; - 15\). Chọn S

TXĐ:\[D = \left[ { - 3;3} \right]\], hàm số liên tục trên \[D = \left[ { - 3;3} \right]\]

+ Ta có:\[y' = \frac{x}{{\sqrt {9 - {x^2}} }},\forall x \in \left( { - 3;3} \right)\] và\[y' = 0 \Leftrightarrow x = 0 \in \left( { - 3;3} \right)\]

+ Với: \[y\left( { - 3} \right) = y\left( 3 \right) = 2;y\left( 0 \right) =  - 1\]

Vậy gía trị lớn nhất và nhỏ nhất của hàm số lần lượt là \[2\]và \[ - 1\]. Chọn Đ

Ta có: \(y' = \frac{{x - 2 - x - 4}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - 6}}{{{{\left( {x - 2} \right)}^2}}} < 0\), \(\;\forall x \in \left[ {3;4} \right]\)

\( \Rightarrow \) Hàm số \(y = \frac{{x + 4}}{{x - 2}}\) nghịch biến trên đoạn \(\left[ {3;4} \right]\).

\( \Rightarrow \mathop {\max }\limits_{\left[ {3;4} \right]} y = y\left( 3 \right) = \frac{{3 + 4}}{{3 - 2}} = 7\). Chọn S

Ta có \(f'\left( x \right) =  - 3{x^2} - 3 < 0\;\forall \;x \in \mathbb{R}\).

Suy ra hàm số \(y = f\left( x \right)\)nghịch biến trên \(\mathbb{R}\).

Suy ra \(f\left( x \right) \le f\left( { - 2} \right)\;\forall \;x \in \left[ { - 2;0} \right]\).

Vậy \(\mathop {\max }\limits_{\left[ { - 2;0} \right]} f\left( x \right) = f\left( { - 2} \right) = 14\). Chọn Đ

Ta có \(y' =  - 8{x^3} + 8x\)

\(\begin{array}{l}y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left( { - 2;1} \right)\\x =  - 1 \in \left( { - 2;1} \right)\\x = 1 \notin \left( { - 2;1} \right)\end{array} \right.\\ \Rightarrow y\left( 0 \right) = 5;y\left( { - 1} \right) = 7;y\left( 1 \right) = 7;y\left( { - 2} \right) =  - 11.\end{array}\)

Chọn S

Ta có \(f'\left( x \right) =  - 4{x^3} + 24x\).

\(f'\left( x \right) = 0 \Leftrightarrow  - 4{x^3} + 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - 1;2} \right]\\x = \sqrt 6  \notin \left[ { - 1;2} \right]\\x =  - \sqrt 6  \notin \left[ { - 1;2} \right]\end{array} \right.\).

\(f\left( { - 1} \right) = 12,\,f\left( 2 \right) = 33,\,f\left( 0 \right) = 1.\)

Vậy \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 2 \right) = 33\). Chọn Đ

TXĐ: \(D = \left[ {0;5} \right]\).

Ta có: \(y' = \frac{{ - 2x + 5}}{{2\sqrt { - {x^2} + 5x} }}\); \(y' = 0 \Leftrightarrow  - 2x + 5 = 0\)\( \Leftrightarrow x = \frac{5}{2}\)

Có: \(y\left( 0 \right) = y\left( 5 \right) = 0\); \(y\left( {\frac{5}{2}} \right) = \frac{5}{2}\).

Vậy \[\max y = y\left( {\frac{5}{2}} \right) = \frac{5}{2}\]. Chọn S

Ta có \(y' = \frac{3}{{{{\left( {x + 1} \right)}^2}}} > 0\) \(\forall x \in \left[ {0;\,2} \right]\) nên hàm số đồng biến trên \(\left[ {0;\,2} \right]\).

Suy ra \(\mathop {\min }\limits_{\left[ {0;\,2} \right]} f\left( x \right) = f\left( 0 \right) =  - 2\). Chọn S

Ta có \[y' = 3{x^2} - 6x - 9\].

\[y' = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 3\end{array} \right.\].

Xét \[y\left( { - 1} \right) = 45,\,y\left( 3 \right) = 13,\,y\left( 5 \right) = 45,\,y\left( { - 5} \right) =  - 115\].

Vậy giá trị lớn nhất và nhỏ nhất lần lượt là \[45;\, - 115\]. Chọn Đ

Ta có \(y' = 3{x^2} - 3 = 0 \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ { - 3;\,\,3} \right]\\x =  - 1 \in \left[ { - 3;\,\,3} \right]\end{array} \right.\).

\(\left. \begin{array}{l}y\left( { - 3} \right) =  - 15\\y\left( { - 1} \right) = 5\\y\left( 1 \right) = 1\\y\left( 3 \right) = 21\end{array} \right\} \Rightarrow \mathop {\min y}\limits_{\left[ { - 3;\,\,3} \right]}  =  - 15\).

Chọn S

Ta có \(y' = 3{x^2} - 2x - 8\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2 \in \left[ {1;3} \right]\\x =  - \frac{4}{3} \notin \left[ {1;3} \right]\end{array} \right.\).

\(y\left( 1 \right) =  - 8\), \(y\left( 3 \right) =  - 6\), \(y\left( 2 \right) =  - 12\). Do đó \(\mathop {\max y}\limits_{x \in \left[ {1;3} \right]}  = y\left( 3 \right) =  - 6\). Chọn Đ

Ta có: \[y' = 4{x^3} - 16x\], cho \[y' = 0 \Rightarrow 4{x^3} - 16x = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 2 \notin \left[ { - 1;1} \right]\\x = 2 \notin \left[ { - 1;1} \right]\\x = 0 \in \left[ { - 1;1} \right]\end{array} \right.\].

Khi đó: \[f\left( { - 1} \right) = 10\], \[f\left( 1 \right) = 10\], \[f\left( 0 \right) = 17\].

Vậy \[\mathop {\max }\limits_{\left[ { - 1;1} \right]} y = f\left( 0 \right) = 17\]. Chọn Đ

Hàm số đã xác định và liên tục trên \[\left[ { - 1;3} \right]\].

Ta có \[\left\{ \begin{array}{l}x \in \left( { - 1;3} \right)\\f'\left( x \right) = 4{x^3} - 12x = 4x\left( {{x^2} - 3} \right) = 0\end{array} \right.\]\[ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \sqrt 3 \end{array} \right.\].

Tính \[f\left( { - 1} \right) =  - 6\], \[f\left( 3 \right) = 26\], \[f\left( 0 \right) =  - 1\], \[f\left( {\sqrt 3 } \right) =  - 10\]\[ \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} f\left( x \right) =  - 10\]. Chọn S

Hàm số \[y = {x^3} - 3{x^2} + 3\] xác định và liên tục trên \[\left[ {0;3} \right]\].

\[y' = 3{x^2} - 6x\], \[y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\], \[f\left( 0 \right) = 3\], \[f\left( 2 \right) =  - 1\], \[f\left( 3 \right) = 3\].

Vậy giá trị lớn nhất của hàm số là \[3\]. Chọn Đ

Hàm số xác định và liên tục trên \(\left[ { - 1;\;3} \right]\). Ta có \(y' = 4{x^3} - 16x\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x =  - 2\; \notin \left[ { - 1;3} \right]\end{array} \right.\).

Khi đó \(y\left( { - 1} \right) =  - 4\), \(y\left( 0 \right) = 3\), \(y\left( 2 \right) =  - 13\), \(y\left( 3 \right) = 12\)\( \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} y = y\left( 2 \right) =  - 13\). Chọn S

Ta có \(y' = 3{x^2} - 4x - 7\), \(y' = 0\) \( \Leftrightarrow x =  - 1\) (nhận) hoặc \(x = \frac{7}{3}\) (loại).

\(y\left( { - 2} \right) =  - 1,\)\(y\left( 1 \right) =  - 7,\)\(y\left( { - 1} \right) = 5\). Vậy \(\mathop {\max }\limits_{x \in \left[ { - 2;1} \right]} y = y\left( { - 1} \right) = 5\). Chọn Đ

Ta có \(f'\left( x \right) = 3{x^2} - 16x + 16\)\( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 16x + 16 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = \frac{4}{3}\end{array} \right.\).

\(f\left( 1 \right) = 0\), \(f\left( 3 \right) =  - 6\), \(f\left( 4 \right) =  - 9\).

Vậy \(\mathop {\max }\limits_{\left[ {1;\,3} \right]} f\left( x \right) = \frac{{13}}{{27}}\). Chọn S

Xét trên đoạn \(\left[ {0;3} \right]\), ta có \[y' = \frac{2}{{{{\left( {x + 1} \right)}^2}}} > 0\], \[\forall x \in \left[ {0;3} \right]\].

Hàm số luôn đồng biến trên khoảng \(\left( {0;3} \right)\), do đó: \[\mathop {\min }\limits_{x \in \left[ {0;{\rm{ 3}}} \right]} y = y\left( 0 \right)\]\[ =  - 1\]. Chọn S

\[D = \mathbb{R}\]. Hàm số liên tục trên \[\left[ { - 1;2} \right]\]

\[f'\left( x \right) = 3{x^2} + 3 > 0\forall x \in \mathbb{R}\]vậy hàm số luôn đồng biến trên tập xác định.

Vậy \[\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) =  - 4\]. Chọn S

Xét trên đoạn \(\left[ { - 2;\frac{1}{2}} \right]\).

\(y' = \frac{{{x^2} - 2x}}{{x - 1}}\);\(y' = 0\)\( \Leftrightarrow x = 0\).

\(y\left( { - 2} \right)\)\( =  - \frac{{13}}{3}\); \(y\left( 0 \right)\)\( =  - 3\); \(y\left( {\frac{1}{2}} \right)\)\( =  - \frac{7}{2}\).

Giá trị lớn nhất của hàm số \(y = \frac{{{x^2} - 3x + 3}}{{x - 1}}\)trên đoạn \(\left[ { - 2;\frac{1}{2}} \right]\)là \( - 3\). Chọn Đ

Ta có \(y' =  - \frac{8}{{{{\left( {x - 3} \right)}^2}}} < 0\)với \[\forall x \in \left[ {0;2} \right]\]. \(y\left( 0 \right) = \frac{1}{3}\), \(y\left( 2 \right) =  - 5\).

Vậy \(\mathop {\max }\limits_{\left[ {0;2} \right]} y = y\left( 0 \right) = \frac{1}{3}\). Chọn Đ

Ta có: \(y' = 3{x^2} - 6x\), \(y' = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ {0;\,4} \right]\\x = 2 \in \left[ {0;\,4} \right]\end{array} \right.\).

Ta có :\(\left\{ \begin{array}{l}y\left( 0 \right) = 2\\y\left( 2 \right) =  - 2\\y\left( 4 \right) = 18\end{array} \right.\). Vậy giá trị lớn nhất của hàm số bằng \(18\). Chọn Đ

Ta có:\[y' = 3{x^2} - 6x - 9\]

Cho\[y' = 0 \Rightarrow 3{x^2} - 6x - 9 = 0 \Rightarrow \left[ \begin{array}{l}x =  - 1\\x = 3\end{array} \right.\]

Mặt khác: \[y\left( { - 2} \right) =  - 4;y\left( { - 1} \right) = 3;y\left( 3 \right) =  - 29;y\left( 4 \right) =  - 22\]

Vậy \[\mathop {Min}\limits_{\left[ { - 2;4} \right]}  =  - 29\].  Chọn Đ

Hàm số liên tục trên đoạn \(\left[ {1;3} \right]\) và có đạo hàm \(f'(x) = 1 - \frac{4}{{{x^2}}}\)

\(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 2(N)}\\{x =  - 2(L)}\end{array}} \right.\)

\(f(1) = 5;f(2) = 4;f(3) = \frac{{13}}{3}\).Suy ra \(M = 5,m = 4.\)

Vậy \(M.m = 20.\) Chọn Đ

Tập xác định: \(D = \left[ { - 2;2} \right]\)

Ta có: \(y' = \frac{{ - x}}{{\sqrt {4 - {x^2}} }}\) \( \Rightarrow y' = 0 \Leftrightarrow x = 0 \in \left( { - 2;2} \right)\)

Ta có: \(\left\{ \begin{array}{l}y\left( { - 2} \right) = y\left( 2 \right) = 0\\y\left( 0 \right) = 2\end{array} \right. \Rightarrow \mathop {\max }\limits_{\left[ { - 2;\,2} \right]} y = 2\). Chọn S

\(y' = 3{x^2} - 4 = 0 \Rightarrow x =  \pm 2 \in \left[ { - 2;3} \right]\).

\(y\left( { - 2} \right) = 17;y\left( 2 \right) =  - 15;y\left( 3 \right) =  - 8\).

\[\mathop { \Rightarrow \min y}\limits_{\left[ { - 2;3} \right]}  =  - 15;\mathop {\max y}\limits_{\left[ { - 2;3} \right]}  = 17\]. Chọn S

Hàm số xác định và liên tục trên đoạn \(\left[ {\frac{1}{2};2} \right]\).

Ta có \(y' = 2x - \frac{2}{{{x^2}}} = \frac{{2{x^3} - 2}}{{{x^2}}}\); \(y' = 0 \Leftrightarrow 2{x^3} - 2 = 0\)\( \Leftrightarrow x = 1\).

\(y\left( {\frac{1}{2}} \right) = \frac{{17}}{4}\); \(y\left( 1 \right) = 3\); \(y\left( 2 \right) = 5\).

Vậy \(m = 3\). Chọn Đ

Tập xác định: \[D = \mathbb{R}\backslash \left\{ 1 \right\}\].

\(y' = \frac{3}{{{{\left( {1 - x} \right)}^2}}} > 0\forall x \in D\). Suy ra hàm số đồng biến trên các khoảng xác định, do đó hàm số cũng đồng biến trên \(\left[ {2;3} \right]\). Vậy giá trị nhỏ nhất của hàm số trên \(\left[ {2;3} \right]\)bằng \(y\left( 2 \right) =  - 5\). Chọn Đ

Ta có \(y' =  - 3{x^2} + 6x\). Khi đó \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\,\left( l \right)\\x = 0\,\,\,\left( n \right)\end{array} \right.\).

\(y\left( { - 3} \right) = 64\); \(y\left( 0 \right) = 10\); \(y\left( 1 \right) = 12\)

Giá trị lớn nhất của hàm số là \(64\). Chọn Đ

Ta có: \(y' =  - 4{x^3} + 4x\).

Cho \(y' = 0\)\( \Leftrightarrow  - 4{x^3} + 4x = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left( {0;3} \right)\\x = 1 \in \left( {0;3} \right)\\x =  - 1 \notin \left( {0;3} \right)\end{array} \right.\).

\( \Rightarrow y\left( 0 \right) = 2\); \(y\left( 1 \right) = 3\); \(y\left( 3 \right) =  - 61\).

Vậy giá trị lớn nhất của hàm số là \(3\). Chọn S

Ta có : \(y' = 2x - \frac{2}{{{x^2}}} = \frac{{2{x^3} - 2}}{{{x^2}}}\) ; \(y' = 0 \Leftrightarrow x = 1\).

Lập bảng biến thiên, suy ra giá trị nhỏ nhất của hàm số bằng \(y\left( 1 \right) = 3\). Chọn Đ

\(f\left( x \right) = x - 5 + \frac{1}{x}\), \(x \in \left( {0; + \infty } \right)\). Khi đó \(f'\left( x \right) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\) ; \(f'\left( x \right) = 0\) \( \Rightarrow \) \(x = 1\).

Ta có bảng biến thiên của hàm số:

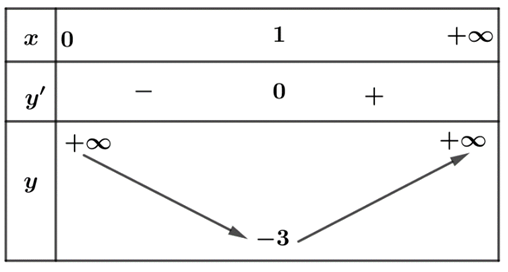
Khi đó ta có \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} {\mkern 1mu} f\left( x \right) = f\left( 1 \right) =  - 3\). Chọn Đ

Hàm số xác định và liên tục trên \(\left( {0; + \infty } \right)\).

Xét \(y' = 3{x^2} - \frac{3}{{{x^2}}} = \frac{{3{x^4} - 3}}{{{x^2}}}\);

\(y' = 0 \Rightarrow \left\{ \begin{array}{l}3{x^4} - 3 = 0\\x \in \left( {0; + \infty } \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  \pm 1\\x \in \left( {0; + \infty } \right)\end{array} \right. \Leftrightarrow x = 1\).

Ta có \(\left\{ \begin{array}{l}y\left( 1 \right) = 4\\\mathop {\lim y}\limits_{x \to {0^ + }}  =  + \infty \\\mathop {\lim y}\limits_{x \to  + \infty }  =  + \infty \end{array} \right.\)\( \Rightarrow m = \mathop {\min }\limits_{\left( {0; + \infty } \right)} y = 4\) tại \(x = 1\). Chọn Đ

Tập xác định : \[D = \left[ { - 2; + \infty } \right)\]. Ta có \[y' = \frac{1}{{2\sqrt {x + 2} }} - 1 = \frac{{1 - 2\sqrt {x + 2} }}{{2\sqrt {x + 2} }}\]; \[y' = 0 \Leftrightarrow x =  - \frac{7}{4}\].

Bảng biến thiên

Vậy giá trị lớn nhất của hàm số là \[\frac{9}{4}\]. Chọn Đ

TXĐ: \(D = \mathbb{R}\). Ta có \(y' = \frac{{\sqrt {{x^2} + 1}  - \frac{{x\left( {x - 1} \right)}}{{\sqrt {{x^2} + 1} }}}}{{{x^2} + 1}} = \frac{{x + 1}}{{\left( {{x^2} + 1} \right)\sqrt {{x^2} + 1} }}\)

\(y' = 0\)\( \Leftrightarrow x + 1 = 0\)\( \Leftrightarrow x =  - 1\).

Bảng biến thiên:

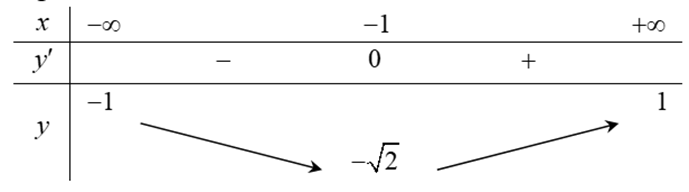
Từ bảng biến thiên ta có \(\mathop {\min }\limits_\mathbb{R} y =  - \sqrt 2 \). Chọn Đ

Xét \(f\left( x \right) = \frac{{3{x^2} - 8x + 6}}{{{x^2} - 2x + 1}}\).

\(f'\left( x \right) = \frac{{2\left( {x - 1} \right)\left( {x - 2} \right)}}{{{{\left( {x - 1} \right)}^4}}}\).

Bảng biến thiên

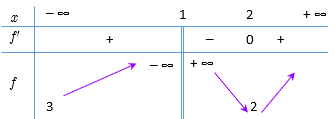
Vậy giá trị nhỏ nhất của \(A\)là \(2\). Chọn S

Đặt \[t = x + 1\], ta có với mọi \[x \in \left[ { - 1;0} \right] \Rightarrow t \in \left[ {0;1} \right]\].

Dựa vào đồ thị ta có: \[a = \mathop {\mathop {\min }\limits_{\left[ {0;1} \right]} f(t)}\limits_{}  = 0\], \[A = \mathop {\mathop {\max }\limits_{\left[ {0;1} \right]} f(t)}\limits_{}  = 3\].

Do đó \[a + A = 3\]. Chọn S

Đặt \[t = x + 1\], ta có với mọi \[x \in \left[ { - 1;0} \right] \Rightarrow t \in \left[ {0;1} \right]\].

Dựa vào đồ thị ta có: \[a = \mathop {\mathop {\min }\limits_{\left[ {0;1} \right]} f(t)}\limits_{}  = 0\], \[A = \mathop {\mathop {\max }\limits_{\left[ {0;1} \right]} f(t)}\limits_{}  = 3\].

Do đó \[a + A = 3\]. Chọn S

Từ đồ thị ta thấy \(M = 2,\;m =  - 4\). Do đó \(M + m = 2 - 4 =  - 2\). Chọn S

Đặt \({\rm{co}}{{\rm{s}}^2}x = t\), với \(t \in \left[ {0\,;\,1} \right]\). Khi đó ta có : \(y = f\left( t \right) = {t^2} - t + 4\).

Xét trên \(\left[ {0\,;\,1} \right]\) ta có :

\(y' = 2t - 1\).

\(y' = 0 \Leftrightarrow t = \frac{1}{2}\).

\(y\left( 0 \right) = 4;\,y\left( 1 \right) = 4;\,y\left( {\frac{1}{2}} \right) = \frac{{15}}{4}\).

Vậy \[\mathop {{\rm{max}}}\limits_\mathbb{R} f\left( x \right) = 4 = f\left( {\frac{\pi }{4}} \right)\]. Chọn S

Xét hàm số \(f\left( t \right) = {t^2} - \sqrt 2 t + 2 + \sqrt 2 \), với \(t = {\cos ^2}x\); \(t \in \left[ {0;\,\,1} \right]\).

\(f'\left( t \right) = 2t - \sqrt 2 \); \(f'\left( t \right) = 0 \Leftrightarrow t = \frac{{\sqrt 2 }}{2}\)

Khi đó \(f\left( 0 \right) = 2 + \sqrt 2 \); \(f\left( 1 \right) = 3\); \(f\left( {\frac{{\sqrt 2 }}{2}} \right) = \frac{3}{2} + \sqrt 2 \)

Vậy \(\mathop {\max }\limits_\mathbb{R} y = \mathop {\max }\limits_\mathbb{R} f\left( t \right) = f\left( 0 \right) = 2 + \sqrt 2 \). Chọn S

Đặt \(t = \sin x,t \in \left[ { - 1;1} \right]\). Xét \(f(t) = {t^2} - 4t - 5\),\(t \in \left[ { - 1;1} \right]\).

\(f'(t) = 2t - 4 = 0 \Leftrightarrow t = 2 \notin \left[ { - 1;1} \right]\).

\(f\left( 1 \right) =  - 8,f\left( { - 1} \right) = 0\).

Ta thấy \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = f\left( 1 \right) =  - 8\). Vậy giá trị nhỏ nhất của hàm số là \[ - 8\]. Chọn Đ

Ta có \(y = {\sin ^3}x - {\rm{cos2}}x + {\mathop{\rm s}\nolimits} {\rm{inx}} + 2\)

\(\,\,\,\, = {\sin ^3}x - \left( {1 - 2{{\sin }^2}x} \right) + {\mathop{\rm s}\nolimits} {\rm{inx}} + 2\)

\(\,\,\,\, = {\sin ^3}x + 2{\sin ^2}x + {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\)

Đặt \(t = {\mathop{\rm s}\nolimits} {\rm{inx;}}\,\,{\rm{t}} \in \left[ { - 1\,;\,1} \right]\). Đưa về bài toán tìm trị nhỏ nhất của hàm số\(f(t) = {t^3} + 2{t^2} + t + 1\) trên \(\left[ { - 1\,;\,1} \right]\).

Ta có \(f'(t) = 3{t^2} + 4t + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t =  - 1 \in \left[ { - 1\,;\,1} \right]}\\{t = \frac{{ - 1}}{3} \in \left[ { - 1\,;\,1} \right]}\end{array}} \right.\).

Mà \(f\left( { - 1} \right) = 1;\,f\left( {\frac{{ - 1}}{3}} \right) = \frac{{23}}{{27}};\,f\left( 1 \right) = 5\) nên giá trị nhỏ nhất của hàm số là \(\frac{{23}}{{27}}\). Chọn Đ

Ta có: \(y = {\cos ^3}x + 2{\sin ^2}x + \cos x = {\cos ^3}x - 2{\cos ^2}x + \cos x + 2\)

Đặt \(t = \cos \,x\), điều kiện: \(t \in \left[ { - 1\,;\,1\,} \right]\).

Khi đó: \(y = f\left( t \right) = {t^3} - 2{t^2} + t + 2\)xét với \(t \in \left[ { - 1\,;\,1\,} \right]\).

Ta có: \(f'\left( t \right) = 3{t^2} - 4t + 1\,\); \(f'\left( t \right) = 0 \Leftrightarrow 3{t^2} - 4t + 1\, = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1 \in \left[ { - 1;\,1\,} \right]\\t = \frac{1}{3} \in \left[ { - 1;\,1\,} \right]\end{array} \right.\)

Lại có: \(f\left( { - 1} \right) =  - 2\,;\,f\left( 1 \right) = 2\,;\,f\left( {\frac{1}{3}} \right) = \frac{{58}}{{27}}\).

Nên \(\max y = \frac{{58}}{{27}}\). Chọn S

Hàm số \(y = {x^4} - 2{x^2} - 3\) liên tục trên đoạn \(\left[ { - 1\,;\,2} \right]\).

\(y' = 4{x^3} - 4x\).

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\, \in \left[ { - 1\,;\,2} \right]\\x =  \pm 1\, \in \left[ { - 1\,;\,2} \right]\end{array} \right.\).

\(y\left( 0 \right) =  - 3\), \(y\left( { - 1} \right) = y\left( 1 \right) =  - 4\), \(y\left( 2 \right) = 5\).

Vậy \(\mathop {\min }\limits_{\left[ { - 1\,;\,2} \right]} y =  - 4\) khi \(x =  \pm 1\). Chọn Đ

Xét hàm số \[y = \frac{{2x + 1}}{{x - 1}}\] liên tục trên đoạn \[\left[ { - 1;0} \right]\].

Có \[y' = \frac{{ - 3}}{{{{\left( {x - 1} \right)}^2}}} < 0\], \[\forall x \in \left[ { - 1;0} \right]\].

Ta có \[y\left( { - 1} \right) = \frac{1}{2}\], \[y\left( 0 \right) =  - 1\]. Do đó \[\mathop {\max }\limits_{\left[ { - 1;0} \right]} y = \frac{1}{2}\], \[\mathop {\min }\limits_{\left[ { - 1;0} \right]} y =  - 1\].

Vậy tích của giá trị lớn nhất và giá trị nhỏ nhất là \[\frac{1}{2}.\left( { - 1} \right) = \frac{{ - 1}}{2}\]. Chọn S

Hàm số \[y = \frac{{{x^2} - 2x + 1}}{{x + 2}}\] có TXĐ: \[\mathbb{R}\backslash \left\{ { - 2} \right\}\] nên hàm số liên tục trên đoạn \(\left[ {0;3} \right]\)

\[y' = \frac{{{x^2} + 4x - 5}}{{{{\left( {x + 2} \right)}^2}}}\]

\[y' = 0 \Leftrightarrow {x^2} + 4x - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {0;3} \right]\\x =  - 5 \notin \left[ {0;3} \right]\end{array} \right.\]

Ta có \(y(0) = \frac{1}{2};\,\,y(3) = \frac{4}{5}\,;\,y(1) = 0\)

Vậy \(\mathop {\max }\limits_{\left[ {0;3} \right]} y = \frac{4}{5}\,\,khi\,x = 3\). Chọn Đ

Hàm số \(y = x + \frac{9}{x}\) liên tục trên đoạn \(\left[ {2;4} \right]\).

Ta có: \(y' = 1 - \frac{9}{{{x^2}}} = \frac{{{x^2} - 9}}{{{x^2}}}\).

Giải \(y' = 0 \Rightarrow {x^2} - 9 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left( {2;4} \right)\\x =  - 3 \notin \left( {2;4} \right)\end{array} \right.\).

Khi đó: \(y\left( 2 \right) = \frac{{13}}{2};{\rm{ }}y\left( 3 \right) = 6;{\rm{ }}y\left( 4 \right) = \frac{{25}}{4}\).

Giá trị nhỏ nhất của hàm số \(y = x + \frac{9}{x}\) trên đoạn \(\left[ {2;4} \right]\) là \(\mathop {\min }\limits_{\left[ {2;4} \right]} y = y\left( 3 \right) = 6\). Chọn Đ

\(D = R\backslash \{  - 2\} \).

Xét trên đoạn \[\left[ {0;3} \right]\], ta có:

\[y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}} > 0\], \[\forall x \in \left[ {0;3} \right]\].

Suy ra hàm số đồng biến trên \[\left[ {0;3} \right]\].

Nên \(M = f(3) = 1\); \(m = f(0) =  - \frac{1}{2}\).

\[M + m = 1 - \frac{1}{2} = \frac{1}{2}\]. Chọn Đ

Ta có \(y' = f'\left( x \right) = 4{x^3} - 4x\)

\(y' = 0 \Leftrightarrow 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left( {0;2} \right)\\x =  - 1 \notin \left( {0;2} \right)\\x = 1 \in \left( {0;2} \right)\end{array} \right.\).

\(f\left( 0 \right) = 1\), \(f\left( 1 \right) = 0\), \(f\left( 2 \right) = 9\).

Vậy \(M = 9.\) Chọn S

Ta có \(f\left( x \right) = {x^3} - 3x + 4\) là hàm đa thức nên liên tục trên \(\mathbb{R}\), vì thế liên tục trên đoạn \(\left[ { - 2;2} \right]\).

\(f'\left( x \right) = 3{x^2} - 3\), \(f'\left( x \right) = 0\)\( \Leftrightarrow 3{x^2} - 3 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 1 \in \left( { - 2;2} \right)\\x = 1 \in \left( { - 2;2} \right)\end{array} \right.\).

Lại có: \(f\left( { - 2} \right) = 2\); \(f\left( { - 1} \right) = 6\); \(f\left( 1 \right) = 2\); \(f\left( 2 \right) = 6\).

Suy ra \(\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 6\) khi \(x =  - 1\) hoặc \(x = 2\). Chọn S

Ta có \[f'\left( x \right) = \frac{2}{{{{\left( {x + 2} \right)}^2}}} > 0,\forall x \ne  - 2\].

Suy ra hàm số đồng biến trên \(\left( { - \infty ; - 2} \right)\)và \(\left( { - 2; + \infty } \right)\). Nên hàm số đồng biến trên \(\left[ {1;4} \right]\).

Vậy \(\mathop {\max }\limits_{\left[ {1;4} \right]} f\left( x \right) = f\left( 4 \right) = \frac{2}{3}\). Chọn S

Ta có hàm số \[f\left( x \right)\]xác định và liên tục trên đoạn \[\left[ {0;\,2} \right]\].

\[f'\left( x \right) = 3{x^2} - 4x + 1\].

\[f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 4x + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{1}{3}\end{array} \right.\].

Mà \[f\left( 0 \right) = 1;\,\,f\left( {\frac{1}{3}} \right) = \frac{{31}}{{27}};\,\,f\left( 1 \right) = 1;\,\,f\left( 2 \right) = 3\].

Suy ra \[M = 3;\,\,m = 1\]. Vậy \[M + m = 4\]. Chọn Đ

Tập xác định: \(D = \left[ { - 2;2} \right]\).

\[y = x + \sqrt {12 - 3{x^2}}  \Rightarrow y' = 1 - \frac{{3x}}{{\sqrt {12 - 3{x^2}} }}\].

\[y' = 0 \Leftrightarrow 1 - \frac{{3x}}{{\sqrt {12 - 3{x^2}} }} = 0 \Leftrightarrow 1 = \frac{{3x}}{{\sqrt {12 - 3{x^2}} }} \Leftrightarrow 3x = \sqrt {12 - 3{x^2}} \,\,\,\left( * \right)\].

Điều kiện: \(x \ge 0\).

\[\left( * \right) \Leftrightarrow 9{x^2} = 12 - 3{x^2}\, \Leftrightarrow 12{x^2} = 12\,\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\,\,\left( {loai} \right)\end{array} \right.\]

Ta có: \(f\left( 1 \right) = 4;\,\,f\left( 2 \right) = 2;\,\,f\left( { - 2} \right) =  - 2\).

Vậy giá trị lớn nhất của hàm số là 2. Chọn S

Xét \(f\left( x \right) = y = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x - 1\).

Ta có \(f'\left( x \right) = {x^2} + x - 2\).

Phương trình \(f'\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 2\end{array} \right.\).

Xét trên đoạn \(\left[ {0\,;\,2} \right]\)ta có \(f\left( 0 \right) =  - 1\); \(f\left( 1 \right) =  - \frac{{13}}{6}\); \(f\left( 2 \right) =  - \frac{1}{3}\).

Vậy \(\mathop {{\rm{max}}}\limits_{\left[ {0\,;\,2} \right]} f\left( x \right) =  - \frac{1}{3}\). Chọn Đ

Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).

Khi đó: \(y' = 1 - \frac{4}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\,\, \in \left[ {1;3} \right]\\x =  - 2 \notin \left[ {1;3} \right]\end{array} \right.\)

Ta có:

\(\begin{array}{l}f\left( 1 \right) = 1 + \frac{4}{1} = 5\\f\left( 2 \right) = 2 + \frac{4}{2} = 4\\f\left( 3 \right) = 3 + \frac{4}{3} = \frac{{13}}{3}\end{array}\)

Vậy \({f_{\min }} = f\left( 2 \right) = 4;\,\,{f_{\max }} = f\left( 3 \right) = 5\). Tích của giá trị nhỏ nhất và giá trị lớn nhất là 20. Chọn S

Ta có \[y' = 3{x^2} - 2x - 1\].

\(y' = 0 \Leftrightarrow 3{x^2} - 2x - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ - 1}}{3} \in \left[ { - 1;\frac{3}{2}} \right]\\x = 1 \in \left[ { - 1;\frac{3}{2}} \right]\end{array} \right.\).

Ta có \(f\left( { - 1} \right) = 0;\,\,f\left( {\frac{{ - 1}}{3}} \right) = \frac{{32}}{{27}};\,\,f\left( 1 \right) = 0;\,\,f\left( {\frac{3}{2}} \right) = \frac{5}{8}\).

Do đó \(m = 0;\,\,M = \frac{{32}}{{27}}\). Suy ra \(M + m = \frac{{32}}{{27}}\). Chọn S

Ta có \(f'\left( x \right) = 3{x^2} - 6x\).

\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \notin \left[ {1;4} \right]\\x = 2 \in \left[ {1;4} \right]\end{array} \right.\).

Ta có \(f\left( 1 \right) = 2\); \(f\left( 2 \right) = 0\); \(f\left( 4 \right) = 20\).

Do đó ta có \(m = \mathop {\min }\limits_{\left[ {1;4} \right]} f\left( x \right) = \min \left\{ {f\left( 1 \right);f\left( 2 \right);f\left( 4 \right)} \right\} = f\left( 2 \right) = 0\).

\(M = \mathop {\max }\limits_{\left[ {1;4} \right]} f\left( x \right) = \max \left\{ {f\left( 1 \right);f\left( 2 \right);f\left( 4 \right)} \right\} = f\left( 4 \right) = 20\).

Suy ra \(M + m = 20 + 0 = 20\). Chọn S

TXĐ \(D = \mathbb{R}\).

Hàm số liên tục trên đoạn \[\left[ { - 1;1} \right]\].

Ta có \(y' =  - 3{x^2} + 6x\)

\(y' = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \in \left[ { - 1;1} \right]\\x = 2 \notin \left[ { - 1;1} \right].\end{array} \right.\)

\(y\left( 0 \right) = 2\); \(y\left( { - 1} \right) = 6\); \(y\left( 1 \right) = 4\).

Vậy \[M + m = 6 + 2 = 8\]. Chọn Đ

Hàm số \(f\left( x \right) = 2{x^2} - \ln x\)xác định và liên tục trên đoạn \(\left[ {\frac{1}{{\rm{e}}};{\rm{e}}} \right]\).

\(f'\left( x \right) = 4x - \frac{1}{x} = \frac{{4{x^2} - 1}}{x}.\)

Xét \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{2} \in \left( {\frac{1}{{\rm{e}}};{\rm{e}}} \right)\\x =  - \frac{1}{2} \notin \left( {\frac{1}{{\rm{e}}};{\rm{e}}} \right)\end{array} \right..\)

Ta có \(f\left( {\frac{1}{{\rm{e}}}} \right) = \frac{2}{{{{\rm{e}}^2}}} + 1;{\rm{ }}f\left( {\rm{e}} \right) = 2{{\rm{e}}^2} - 1;{\rm{ }}f\left( {\frac{1}{2}} \right) = \frac{1}{2} + \ln 2.\)

Suy ra \[\mathop {\max }\limits_{\left[ {\frac{1}{{\rm{e}}};{\rm{e}}} \right]} f\left( x \right) = f\left( {\rm{e}} \right) = 2{{\rm{e}}^2} - 1;{\rm{ }}\mathop {\min }\limits_{\left[ {\frac{1}{{\rm{e}}};{\rm{e}}} \right]} f\left( x \right) = \frac{1}{2} + \ln 2.\]

Vậy \[\mathop {\max }\limits_{\left[ {\frac{1}{{\rm{e}}};{\rm{e}}} \right]} f\left( x \right) - \mathop {\min }\limits_{\left[ {\frac{1}{{\rm{e}}};{\rm{e}}} \right]} f\left( x \right) = 2{{\rm{e}}^2} + \ln 2 - \frac{3}{2}.\] Chọn Đ

Xét hàm số \(y = {x^2} + \frac{2}{x}\) xác định và liên tục trên \(\left[ {\frac{1}{2};2} \right]\)

\(y' = 2x - \frac{2}{{{x^2}}}\)

Xét trên khoảng \(\left( {\frac{1}{2};2} \right)\), phương trình \(y' = 0\) có nghiệm \(x = 1\).

\(y\left( {\frac{1}{2}} \right) = \frac{{17}}{4}\); \(y\left( 1 \right) = 3\); \(y\left( 2 \right) = 5\).

Vậy \(\mathop {\min }\limits_{\left[ {\frac{1}{2};1} \right]} y = y\left( 1 \right) = 3\) và \(\mathop {\max }\limits_{\left[ {\frac{1}{2};1} \right]} y = y\left( 2 \right) = 5\). Tích giá trị lớn nhất và giái trị nhỏ nhất của hàm số \(y = {x^2} + \frac{2}{x}\) trên đoạn \(\left[ {\frac{1}{2};2} \right]\) bằng 15. Chọn S

Hàm số liên tục và xác định trên đoạn \(\left[ { - 2\,;\, - 1} \right]\).

Ta có \(f'\left( x \right) = 1 - \frac{4}{{{x^2}}} = \frac{{{x^2} - 4}}{{{x^2}}}\)\( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow {x^2} - 4 = 0\)\[ \Leftrightarrow \left[ \begin{array}{l}x = 2 \notin \left[ { - 2; - 1} \right]\\x =  - 2 \in \left[ { - 2; - 1} \right]\end{array} \right.\].

Tính \(\left\{ \begin{array}{l}f\left( { - 2} \right) =  - 5\\f\left( { - 1} \right) =  - 6\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}\mathop {max}\limits_{\left[ { - 2\,;\, - 1} \right]} f\left( x \right) =  - 5\,\,{\rm{khi}}\,\,x =  - 2\\\mathop {\min }\limits_{\left[ { - 2\,;\, - 1} \right]} f\left( x \right) =  - 6\,\,{\rm{khi}}\,\,x =  - 1\end{array} \right.\).

Vậy, giá trị nhỏ nhất của hàm số bằng \( - 6\). Chọn S

Hàm số xác định và liên tục trên đoạn \[\left[ {1;\,\,4} \right]\].

Ta có \[f'\left( x \right) = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\]; \[f'\left( x \right) = 0 \Leftrightarrow {x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ {1;\,\,4} \right]\\x =  - 1 \notin \left[ {1;\,\,4} \right]\end{array} \right.\].

\[f\left( 1 \right) = 2\]; \[f\left( 4 \right) = \frac{{17}}{4}\]. Suy ra \[m = \mathop {\min }\limits_{\left[ {1;\,\,4} \right]} f\left( x \right) = f\left( 1 \right) = 2\]; \[M = \mathop {\max }\limits_{\left[ {1;\,\,4} \right]} f\left( x \right) = f\left( 4 \right) = \frac{{17}}{4}\].

Vậy \[m.M = \frac{{17}}{2}\]. Chọn S

Tập xác định: \[D = \left[ {3;5} \right]\]. \(y' = \frac{1}{{2\sqrt {x - 3} }} - \frac{1}{{2\sqrt {5 - x} }}\), \(y' = 0\)\( \Leftrightarrow \sqrt {x - 3}  = \sqrt {5 - x} \)\( \Leftrightarrow x = 4\)

\[y\left( 3 \right) = \sqrt 2 \],\[y\left( 5 \right) = \sqrt 2 \] \[y\left( 4 \right) = 2\].

Dựa vào BBT ta có tập giá trị của hàm số là \(T = \left[ {\sqrt 2 ;2} \right]\). Chọn Đ

Hàm số đã cho liên tục trên đoạn \[\left[ {2;4} \right]\].

Ta có: \[y' = 1 - \frac{9}{{{x^2}}}\]. Cho \[y' = 0\]ta được \[\left[ \begin{array}{l}x =  - 3 \notin \left[ {2;4} \right]\\x = 3 \in \left[ {2;4} \right]\end{array} \right.\]

Khi đó: \[f\left( 2 \right) = \frac{{13}}{2}\], \[f\left( 3 \right) = 6\], \[f\left( 4 \right) = \frac{{25}}{4}\].

Vậy \[\mathop {\min }\limits_{\left[ {2;{\rm{ 4}}} \right]} y = 6\]. Chọn S

\(y = \frac{{\cos x + 1}}{{\sin x + 1}}\).

Vì \[x \in \left[ {0;\frac{\pi }{2}} \right]\]nên \[\sin x \in \left[ {0;1} \right]\]. Do đó hàm số đã cho xác định trên \(\left[ {0;\frac{\pi }{2}} \right]\).

\(y = \frac{{\cos x + 1}}{{\sin x + 1}} \Rightarrow y' = \frac{{ - {{\sin }^2}x - {{\cos }^2}x}}{{{{\left( {\sin x + 1} \right)}^2}}} = \frac{{ - 1}}{{{{\left( {\sin x + 1} \right)}^2}}} < 0\), \(\forall x \in \left[ {0;\frac{\pi }{2}} \right]\).

Suy ra hàm số luôn nghịch biến trên \(\left[ {0;\frac{\pi }{2}} \right]\).

Do đó: \(\mathop {\max }\limits_{\left[ {0;\frac{\pi }{2}} \right]} y = y\left( 0 \right) = 2\); \(\mathop {\min }\limits_{\left[ {0;\frac{\pi }{2}} \right]} y = \frac{1}{2}\).

Vậy tập giá trị của hàm số đã cho là \(\left[ {\frac{1}{2};2} \right]\). Chọn Đ

Hàm số \(f\left( x \right) = {x^4} - 4{x^2} + 5\) xác định và liên tục trên \(\left[ { - 2;3} \right]\).

Ta có: \(f'\left( x \right) = 4{x^3} - 8x\).

Do đó: \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \sqrt 2 \end{array} \right.\).

Mà: \(f\left( 0 \right) = 5\), \(f\left( {\sqrt 2 } \right) = f\left( { - \sqrt 2 } \right) = 1\), \(f\left( { - 2} \right) = 5\), \(f\left( 3 \right) = 50\).

Suy ra: \(\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right) = 50\). Chọn Đ

\(y = {\cos ^3}x + 9\cos x + 6{\rm{si}}{{\rm{n}}^2}x - 1\)\( = {\cos ^3}x + 9\cos x + 6\left( {1 - {{\cos }^2}x} \right) - 1\)\( = {\cos ^3}x - 6{\cos ^2}x + 9\cos x + 5\)

Xét hàm số \(f\left( t \right) = {t^3} - 6{t^2} + 9t + 5\) với \(t = \cos x\) và \(t \in \left[ { - 1;1} \right]\).

Ta có \(f'\left( t \right) = 0 \Leftrightarrow 3{t^2} - 12t + 9 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 3\end{array} \right.\).

Trên đoạn \(\left[ { - 1;1} \right]\) ta có \(f\left( 1 \right) = 9\); \(f\left( { - 1} \right) =  - 11\).

Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho là \(9 - 11 =  - 2\). Chọn Đ

Đặt: \(t = \cos x\)\[ \Rightarrow t \in \left[ { - 1;1} \right]\]\[ \Rightarrow y = 2t - \frac{4}{3}{t^3}\].

\[y' = 2 - 4{t^2}\];\[y' = 0\]\[ \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ - 1}}{{\sqrt 2 }} \in \left[ { - 1;1} \right]\\x = \frac{1}{{\sqrt 2 }} \in \left[ { - 1;1} \right]\end{array} \right.\].

Tính:\[y\left( { - 1} \right) = \frac{{ - 2}}{3}\], \[y\left( {\frac{{ - 1}}{{\sqrt 2 }}} \right) = \frac{{ - 2\sqrt 2 }}{3}\], \[y\left( {\frac{1}{{\sqrt 2 }}} \right) = \frac{{2\sqrt 2 }}{3}\], \[y\left( 1 \right) = \frac{2}{3}\].

Vậy: \(\mathop {\max }\limits_{\left[ {0;\pi } \right]} y = \frac{{2\sqrt 2 }}{3}\). Chọn Đ

Ta có: \(y' = 3{x^2} - 3\). Xét \(y' = 0 \Rightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y =  - 1\\x =  - 1 \Rightarrow y = 3\end{array} \right.\).

Bảng biến thiên:

Ta có: \(y\left( 2 \right) = 3\). Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng \[\left( {1; + \infty } \right)\].

Vì \[m > 0 \Rightarrow 1 < m + 1 < m + 2\]do đó hàm số đồng biến trên \(D = \left[ {m + 1\,;\,m + 2} \right]\).

Suy ra \[\mathop {\min }\limits_{\left[ {m + 1;m + 2} \right]} y = y\left( {m + 1} \right)\]. Để giá trị nhỏ nhất của hàm số trên \(D = \left[ {m + 1\,;\,m + 2} \right]\)luôn bé hơn \(3\)\[ \Leftrightarrow y\left( {m + 1} \right) < 3 = y\left( 2 \right)\]\[ \Leftrightarrow m + 1 < 2\]\[ \Leftrightarrow m < 1\]

Suy rA. \(m \in \left( {0\,;\,1} \right)\). Chọn Đ

Từ giả thiết suy ra tốc độ truyền bệnh tại thời điểm \(t\) là: \(f'\left( t \right) = 90t - 3{t^2}\).

Xét hàm \(f'\left( t \right) = 90t - 3{t^2}\) với \(0 \le t \le 25\).

Ta có: \(f''\left( t \right) = 90 - 6t = 0 \Leftrightarrow t = 15\).

Bảng biến thiên:

Từ bảng biến thiên ta có ngày mà tốc độ truyền bệnh lớn nhất là ngày thứ \(15\). Chọn Đ

Theo ý nghĩa vật lí của đạo hàm, vận tốc tức thời của một vật khi chuyển động là đạo hàm của quãng đường theo thời gian t.

Vận tốc tức thời của vật tại thời điểm \[t\] là \(v(t) = s'(t) = {\left( {\frac{1}{3}{t^3} - {t^2} + 9t} \right)^\prime } = {t^2} - 2t + 9\).

Xét hàm số \(v\left( t \right) = {t^2} - 2t + 9\) trên đoạn từ \[\left[ {0;10} \right]\].

Từ bảng biến thiên giá trị lớn nhất của hàm \[v\left( t \right)\] là 89. Chọn Đ

Ta có \(v = s' =  - \frac{3}{2}{t^2} + 12t =  - \frac{3}{2}\left( {{t^2} - 8t + 16} \right) + 24 = 24 - \frac{3}{2}{\left( {t - 4} \right)^2} \le 24\)

Vậy \(\mathop {\max }\limits_{\left[ {0;\,6} \right]} v\left( t \right) = 24\,\left( {{\rm{m/s}}} \right)\) tại thời điểm \(t = 4\) (giây). Chọn S

Ta có \[v\left( t \right) = s'\left( t \right) =  - {t^2} + 12t\]. Ta tìm GTLN của \[v\left( t \right)\]trên \[\left[ {0;7} \right]\].

\[v'\left( t \right) =  - 2t + 12\], \[v'\left( t \right) = 0 \Leftrightarrow t = 6\]. Khi đó \[v\left( 6 \right) = 36\], \[v\left( 0 \right) = 0\], \[v\left( 7 \right) = 35\].

Vậy vận tốc lớn nhất đạt được bằng \(36\left( {{\rm{m/s}}} \right)\). Chọn Đ

Đặt \(t = \sin x\). Vì \(x \in \left[ { - \frac{\pi }{6};\,\frac{{5\pi }}{6}} \right]\) nên \(t \in \left[ { - \frac{1}{2};1} \right]\).

Khi đó hàm số trở thành: \(f\left( t \right) = \frac{{12}}{{7 - 4t}}\) với \(t \in \left[ { - \frac{1}{2};1} \right]\)

Ta có \(f'\left( t \right) = \frac{{48}}{{{{\left( {7 - 4t} \right)}^2}}} > 0\), \(\forall t \in \left[ { - \frac{1}{2};\,1} \right]\) nên hàm số đồng biến trên \(\left[ { - \frac{1}{2};1} \right]\).

Do đó \[M = \mathop {\max }\limits_{\left[ { - \frac{1}{2};1} \right]} f\left( t \right) = f\left( 1 \right) = 4\] và \[m = \mathop {\min }\limits_{\left[ { - \frac{1}{2};1} \right]} f\left( t \right) = f\left( { - \frac{1}{2}} \right) = \frac{4}{3}\]. Chọn S

Ta có\(f\left( x \right) = \frac{{1 + {{\left( {1 - {{\cos }^2}x} \right)}^2}}}{{2 + {{\cos }^2}x}} + \frac{{1 + 1 - {{\cos }^2}x}}{{2 + {{\cos }^4}x}} = \frac{{2 - 2{{\cos }^2}x + {{\cos }^4}x}}{{2 + {{\cos }^2}x}} + \frac{{2 - {{\cos }^2}x}}{{2 + {{\cos }^4}x}}\)

Đặt \({\cos ^2}x = t \Rightarrow t \in \left[ {0;1} \right]\). Khi đó ta có hàm số \(f(t) = \frac{{2 - 2t + {t^2}}}{{2 + t}} + \frac{{2 - t}}{{2 + {t^2}}}\)với \(t \in \left[ {0;1} \right]\).

Ycbt \( \Leftrightarrow \)Tìm \(\mathop {\max }\limits_{t \in \left[ {0;1} \right]} f\left( t \right) = ?\)

Dễ thấy \(f(t)\)liên tục trên đoạn \(\left[ {0;1} \right]\). (1)

Ta có:

\(f'(t) = {\left( {\frac{{2 - 2t + {t^2}}}{{2 + t}} + \frac{{2 - t}}{{2 + {t^2}}}} \right)^\prime } = \frac{{\left( { - 2 + 2t} \right)\left( {2 + t} \right) - \left( {2 - 2t + {t^2}} \right)}}{{{{\left( {2 + t} \right)}^2}}} + \frac{{ - \left( {2 + {t^2}} \right) - \left( {2 - t} \right)2t}}{{{{\left( {2 + {t^2}} \right)}^2}}}\)

\( = \frac{{{t^2} + 4t - 6}}{{{{\left( {2 + t} \right)}^2}}} + \frac{{{t^2} - 4t - 2}}{{{{\left( {2 + {t^2}} \right)}^2}}} = \frac{{{{\left( {t + 2} \right)}^2} - 10}}{{{{\left( {2 + t} \right)}^2}}} + \frac{{{{\left( {t - 2} \right)}^2} - 6}}{{{{\left( {2 + {t^2}} \right)}^2}}}\)với \(t \in \left[ {0;1} \right]\).

Với\(t \in \left[ {0;1} \right]\)thì \(\frac{{{{\left( {t + 2} \right)}^2} - 10}}{{{{\left( {2 + t} \right)}^2}}} < 0\,\,;\,\,\frac{{{{\left( {t - 2} \right)}^2} - 6}}{{{{\left( {2 + {t^2}} \right)}^2}}} < 0\). Suy rA. \(f'(t) < 0,\forall t \in \left[ {0;1} \right]\)

Suy ra hàm số \(g(t)\)nghịch biến trên đoạn\(\left[ {0;1} \right]\). (2)

Từ (1) và (2) suy rA. \(\mathop {\max }\limits_{t \in \left[ {0;1} \right]} f\left( t \right) = f\left( 0 \right) = 2\). Chọn Đ

TXĐ: \(D = \left[ {1;5} \right]\).

Đặt: \(t = \sqrt {x - 1}  + \sqrt {5 - x} \)\( \Rightarrow \sqrt {x - 1} .\sqrt {5 - x}  = \frac{{{t^2} - 4}}{2}\).

\(t' = \frac{1}{{2\sqrt {x - 1} }} - \frac{1}{{2\sqrt {5 - x} }}\)\( = \frac{{\sqrt {5 - x}  - \sqrt {x - 1} }}{{2\sqrt {x - 1} \sqrt {5 - x} }}\)\( = 0\)\[ \Leftrightarrow \sqrt {5 - x}  = \sqrt {x - 1} \]\[ \Leftrightarrow x = 3\].

\(t\left( 1 \right) = t\left( 5 \right) = 2\); \(t\left( 3 \right) = 2\sqrt 2 \).

Do đó: \(x \in \left[ {1;5} \right]\)\( \Rightarrow t \in \left[ {2;2\sqrt 2 } \right]\).

\(f\left( t \right) = t - \frac{{{t^2} - 4}}{2}\); \(t \in \left[ {2;2\sqrt 2 } \right]\).

\(f'\left( t \right) = 1 - t < 0\); \(\forall t \in \left[ {2;2\sqrt 2 } \right]\)

Vậy \(\mathop {\min }\limits_D y = \mathop {\min }\limits_{\left[ {2;2\sqrt 2 } \right]} f\left( t \right)\)\( = f\left( {2\sqrt 2 } \right)\)\( = 2\sqrt 2  - 2\). Chọn S

Ta có \(v = S' =  - {t^2} + 8t + 9,\)\(t \in \left( {0;\,10} \right)\)

\(v' =  - 2t + 8\). Xét \(v' = 0 \Rightarrow t = 4 \in \left( {0;\,10} \right)\)

Bảng biến thiên:

Vậy vận tốc lớn nhất của chất điểm là \(25\left( {{\rm{m/s}}} \right)\) tại tại \(t = 4.\) Chọn Đ

Gọi \(a\), \(b\), \(h\) \(\left( {a,b,h > 0} \right)\) lần lượt là chiều dài, chiều rộng và chiều cao của bể chứa nước.

Ta có: \(a = 2b\) nên \(V = abh = 2{b^2}.h\) \( \Rightarrow h = \frac{V}{{2{b^2}}}\).

Chi phí thuê nhân công thấp nhất tương đương với diện tích toàn phần của bể ít nhất.

Áp dụng BĐT Cauchy cho 3 số dương \(\frac{{3V}}{{2b}}\), \(\frac{{3V}}{{2b}}\), \(2{b^2}\), ta được:

\({S_{TP}} = \frac{{3V}}{b} + 2{b^2} = \frac{{3V}}{{2b}} + \frac{{3V}}{{2b}} + 2{b^2} \ge 3\sqrt[3]{{\frac{{9{V^2}}}{{4{b^2}}}.2{b^2}}} = 3\sqrt[3]{{\frac{9}{2}{{.288}^2}}} = 216\)\(\left( {{\rm{d}}{{\rm{m}}^2}} \right)\)\( = 2,16\,\left( {{{\rm{m}}^2}} \right)\).

Do đó chi phí thấp nhất thuê nhân công là \(2,16.500000 = 1080000\) (đồng). Chọn Đ

Gọi \(x\)(lít) \(\left( {0 < x < 10} \right)\)là số xăng An sử dụng trong \(1\)ngày.

Khi đó: \(10 - x\)(lít) là số xăng Bình sử dụng trong \(1\)ngày.

Suy ra \(f\left( x \right) = \frac{{32}}{x} + \frac{{72}}{{10 - x}}\,\,,\,\,x \in \left( {0;10} \right)\)là tổng số ngày An và Bình sử dụng hết số xăng được khoán.

Ta có: \(f\left( x \right) = \frac{{32}}{x} + \frac{{72}}{{10 - x}}\)\( \Rightarrow {f^'}\left( x \right) =  - \frac{{32}}{{{x^2}}} + \frac{{72}}{{{{\left( {10 - x} \right)}^2}}}\).

Cho \({f^'}\left( x \right) = 0\)\( \Leftrightarrow  - \frac{{32}}{{{x^2}}} + \frac{{72}}{{{{\left( {10 - x} \right)}^2}}} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 4\\x =  - 20 \notin \left( {0;10} \right)\end{array} \right.\)

Bảng biến thiên của hàm số \(f\left( x \right) = \frac{{32}}{x} + \frac{{72}}{{10 - x}}\,\,,\,\,x \in \left( {0;10} \right)\)

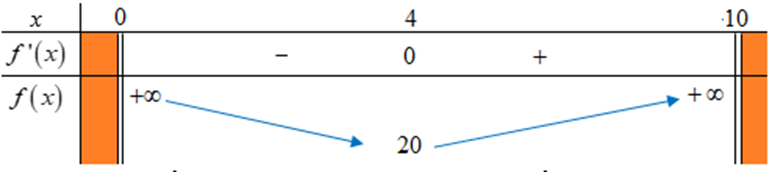
Theo BBT: ít nhất \(20\)ngày thì An và Bình sử dụng hết lượng xăng được khoán. Chọn Đ

Gọi \(x\) (nghìn VNĐ) là số tiền công ty sẽ tăng thêm đối với một khách. Khi đó số khách sẽ giảm đi là \(50x\) khách nên còn \(10.000 - 50x\) khách. Khi đó, \(10.000 - 50x > 0\) \( \Leftrightarrow x < 200\).

Khi đó số tiền thu được sau khi tăng giá vé là \(f\left( x \right) = \left( {50 + x} \right)\left( {10.000 - 50x} \right)\).

Ta có \(f\left( x \right) = 50\left( {50 + x} \right)\left( {200 - x} \right) \le 50{\left( {\frac{{50 + x + 200 - x}}{2}} \right)^2} = 781250\) (nghìn VNĐ).

Vậy số tiền thu được tăng thêm lớn nhất là \(781250 - 50 \times 10.000 = 281.250\) nghìn VNĐ khi \(50 + x = 200 - x\) \( \Leftrightarrow x = 75\) nghìn VNĐ. Chọn S

Gọi \[x\]là chiều dài 1 mặt hàng rào hình chữ E ( trong ba mặt song song,\[x > 0\]).

Gọi \[y\]là chiều dài mặt hàng rào hình chữ E song song với bờ sông (\[y > 0\]).

Số tiền phải làm là:\[x.3.50000 + y.60000 = 15.000.000 \Leftrightarrow y = \frac{{500 - 5x}}{2}\].

Diện tích đất: \[S = x.y = x.\frac{{500 - 5x}}{2} = 250x - \frac{5}{2}{x^2}\]

Ta có: \[S' = 250 - 5x\].

\[S' = 0 \Leftrightarrow 250 - 5x \Leftrightarrow x = 50.\]

Bảng biến thiên:

Vậy: \[\mathop {\max S}\limits_{\left( {0; + \infty } \right)}  = 6250{\rm{ }}({m^2})\] khi \[x = 50.\] Chọn S

Giả sử khối hộp chữ nhật là \(ABCD.A'B'C'D'\)và \(AB = x\), \(AD = 2x\)và \[AA' = h\](\(x,\,h > 0\)).

Ta có \(V = x.2x.h\)\( \Leftrightarrow 2{x^2}h = \frac{{500}}{3}\)\( \Leftrightarrow h = \frac{{250}}{{3{x^2}}}\).

Diện tích cần xây là \(S = 2{x^2} + 2\left( {xh + 2xh} \right)\)\( = 2{x^2} + 6xh\).

Ta cần tìm giá trị nhỏ nhất của \(S = 2{x^2} + \frac{{500}}{x}\)với \(x > 0\).

Ta có \(2{x^2} + \frac{{250}}{x} + \frac{{250}}{x} \ge 3\sqrt[3]{{2{x^2}.\frac{{250}}{x}.\frac{{250}}{x}}}\)\( \Leftrightarrow 2{x^2} + \frac{{250}}{x} + \frac{{250}}{x} \ge 150\).

Dấu đẳng thức xảy ra khi \(2{x^2} = \frac{{250}}{x}\)\( \Leftrightarrow x = 5\).

\(S\)nhỏ nhất là \(150\)khi \(x = 5\).

Số tiền chi phí là \(150.500000 = 75000000\)hay \(75\)triệu đồng. Chọn Đ

Do \(x\)là độ dài của đoạn dây cuộn thành hình tròn \(\left( {0 < x < a} \right)\).

Suy ra chiều dài đoạn còn lại là \(a - x\).

Chu vi đường tròn: \(2\pi r = x\)\( \Rightarrow r = \frac{x}{{2\pi }}\).

Diện tích hình tròn: \({S_1} = \pi .{r^2}\)\( = \frac{{{x^{\rm{2}}}}}{{4\pi }}\).

Diện tích hình vuông: \({S_2} = {\left( {\frac{{a - x}}{4}} \right)^2}\).

Tổng diện tích hai hình: \(S = \frac{{{x^2}}}{{4\pi }} + {\left( {\frac{{a - x}}{4}} \right)^2}\)\( = \frac{{\left( {4 + \pi } \right).{x^2} - 2a\pi x + \pi {a^2}}}{{16\pi }}\).

Đạo hàm: \(S' = \frac{{\left( {4 + \pi } \right).x - a\pi }}{{8\pi }}\); \(S' = 0\)\( \Leftrightarrow x = \frac{{a\pi }}{{4 + \pi }}\).

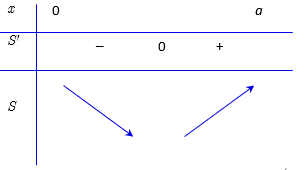
Suy ra hàm \(S\)chỉ có một cực trị và là cực tiểu tại \(x = \frac{{a\pi }}{{4 + \pi }}\).

Do đó \(S\)đạt giá trị nhỏ nhất tại \(x = \frac{{a\pi }}{{4 + \pi }}\). Chọn Đ

Gọi chiều rộng của đáy hồ nước là \(x\)\( \Rightarrow \)chiều dài của đáy hồ nước là \(3x\)\(\left( m \right)\), với \(0 < x < \sqrt 6 \)

Suy ra chiều cao của hồ nước là \(h = \frac{6}{{{x^2}}}\)\(\left( m \right)\)

Tổng diện tích cần xây là \( = 2xh + 2.3xh + 3{x^2}\)\( = 8xh + 3{x^2}\)hay \(S\left( x \right) = \frac{{48}}{x} + 3{x^2}\).

Do đó \(S\left( x \right) = \frac{{24}}{x} + \frac{{24}}{x} + 3{x^2}\)\( \ge 3\sqrt[3]{{\frac{{24}}{x}.\frac{{24}}{x}.3{x^2}}} = 36\), với mọi \(0 < x < \sqrt 6 \).

Vậy \({S_{\min }} = 36\,\,\left( {{m^2}} \right)\)khi \(\frac{{24}}{x} = 3{x^2}\)hay \(x = 2\). Vậy chi phí xây hồ là \(18\)triệu đồng. Chọn Đ

Gọi chiều dài đoạn dây uốn thành hình vuông là \(x\,{\rm{cm}}\). Điều kiện: \(0 \le x \le 60\)

Độ dài cạnh hình vuông là \(\frac{x}{4}\)

Chiều dài đoạn dây uốn thành hình tròn là \(\left( {60 - x} \right)\,{\rm{cm}}\)

Bán kính vòng tròn là \(2\pi R = \left( {60 - x} \right) \Leftrightarrow R = \frac{{60 - x}}{{2\pi }}\)

Tổng diện tích của hình vuông và hình tròn là \({\left( {\frac{x}{4}} \right)^2} + \pi {R^2} = {\left( {\frac{x}{4}} \right)^2} + \pi {\left( {\frac{{60 - x}}{{2\pi }}} \right)^2}\)

\( = {\frac{x}{{16}}^2} + \frac{{{{\left( {60 - x} \right)}^2}}}{{4\pi }} = \frac{{\left( {\pi  + 4} \right){x^2} - 480x + 14400}}{{16\pi }} = f\left( x \right)\)

Hàm số \(f\left( x \right)\) đạt giá trị nhỏ nhất tại \(x = \frac{{480}}{{2\left( {\pi  + 4} \right)}} \approx 33,61\). Chọn S