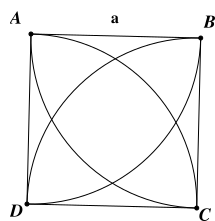
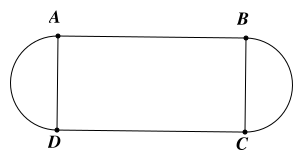
Cho nửa đường tròn \[\left( O \right)\] đường kính \[AB = 2R\]. Lấy \[M\] là điểm chính giữa cung \[AB\], hai điểm \[C\] và \[D\] di chuyển trên cung \[MA,MB\] sao cho \[CM//AD\]. Hỏi độ dài cạnh \[CD\] bằng bao nhiêu?
A. \[\frac{{2R}}{3}\].
B. \[R\sqrt 3 \].
C. \[\frac{{R\sqrt 3 }}{2}\].
D. \[R\sqrt 2 \].
Quảng cáo
Trả lời:
Chọn D
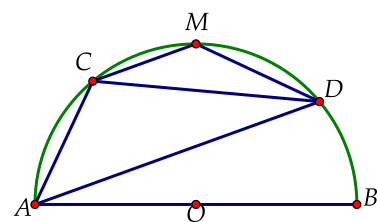
\[M\] là điểm chính giữa của cung \[AB\] nên .
Do \[MC//AD\] nên
\[ \Rightarrow \widehat {COD} = 90^\circ \] (góc ở tâm chắn cung \[CD\])
\[ \Rightarrow \Delta COD\] vuông cân tại \[O \Rightarrow CD = CO\sqrt 2 = R\sqrt 2 \].
Với bài tập này ta cũng có thể lí luận \[ACMD\] là hình thang cân nên \[CD = AM = R\sqrt 2 \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[80^\circ \].
B. \[100^\circ \].
C. \[140^\circ \].
D. \[160^\circ \].
Lời giải
Chọn D
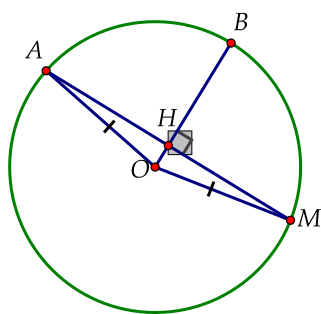
\[\Delta OAM\]cân tại \[O\] \[\left( {OA = OM = R} \right)\].
\[OB \bot AM\]tại \[H\] suy ra \[OB\] đồng thời là đường phân giác của \[\widehat {AOM}\];
\[\widehat {AOB} = \widehat {BOM} = 80^\circ \] \[ \Rightarrow \widehat {AOM} = \widehat {AOB} + \widehat {BOM}\] \[ = 80^\circ + 80^\circ = 160^\circ \].
Do đó số đo của cung nhỏ bằng: \[\widehat {AOM} = 160^\circ \].
Câu 2
A. sđ, sđ.
B. sđ, sđ.
C. sđ, sđ.
D. sđ, sđ.
Lời giải
Chọn D
Vì \[\Delta OAB\]cân tại \[{\rm{O}}\] \[\left( {OA = OB = R} \right)\]\[ \Rightarrow \widehat {OBA} = \widehat {OAB} = 30^\circ \]\[ \Rightarrow \widehat {BOA} = 180^\circ - \widehat {OBA} - \widehat {OAB}\]
\[\widehat {BOA} = 180^\circ - 30^\circ - 30^\circ = 120^\circ \] suy ra số đo cung nhỏ bằng: \[\widehat {BOA} = 120^\circ \].
Vì \[\Delta OCD\]cân tại \[O\] \[\left( {OC = OD = R} \right)\]\[ \Rightarrow \widehat {OCD} = \widehat {ODC} = 40^\circ \]\[ \Rightarrow \widehat {COD} = 180^\circ - \widehat {OCD} - \widehat {ODC}\]
\[\widehat {COD} = 180^\circ - 40^\circ - 40^\circ = 100^\circ \] suy ra số đo cung nhỏ bằng: \[\widehat {COD} = 100^\circ \].
Câu 3
A. \(\frac{a}{2}\).
B. \(\frac{{a\sqrt 3 }}{3}\).
C. \(a\).
D. \(2a\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[R\].
B. \[R\frac{{\sqrt 3 }}{2}\].
C. \[R\sqrt 2 \].
D. \[R\sqrt 3 \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{2}{3}\pi a\).
B. \(\pi a\).
C. \(\frac{1}{3}\pi a\).
D. \(\frac{4}{3}\pi a\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(50\)m.
B. \(63,7\)m.
C. \(31,8\)m.
D. \(78,5\)m.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[240^\circ \].
B. \[120^\circ \].
C. \[360^\circ \].
D. \[210^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Tìm số đo cung nhỏ \[AB\] và cung nhỏ \[CD\] qua hình vẽ sau (ảnh 1)](https://video.vietjack.com/upload2/images/1754926966/1754927034-image20.png)