Cho đường tròn \(\left( {O;R} \right)\) và điểm \(A\) sao cho \(OA = 2R\). Kẻ tiếp tuyến \(AB\) với đường tròn
(\(B\) là tiếp điểm). Độ dài \(AB\) bằng
Quảng cáo
Trả lời:
Chọn D
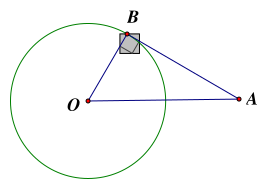
Ta có \(AB\) là tiếp tuyến của đường tròn \(\left( O \right)\)\( \Rightarrow AB \bot OB\).
Xét \(\Delta BAO\left( {\widehat B = 90^\circ } \right):O{B^2} + A{B^2} = O{A^2}\)
\( \Rightarrow AB = \sqrt {O{A^2} - O{B^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = \sqrt {3{R^2}} = R\sqrt 3 \).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn B
Vì \(A( - 2\,;\,3)\) nên khoảng cách từ \(A\) đến trục hoành là \({d_1} = \,|{y_A}|\, = 3\), khoảng cách từ \(A\) đến trục tung là \({d_2} = \,|{x_A}|\, = 2\).
Nhận thấy \({d_2} = R( = 2)\) nên trục tung tiếp xúc với đường tròn \((A;2)\).
Và \({d_2} = 3 > 2 = R\) nên trục hoành không cắt đường tròn \((A;2)\).
Lời giải
Chọn B


Vì tam giác \(ABC\) cân tại \(A\) có \(O\) là tâm đường tròn ngoại tiếp nên đường thẳng \(AO \bot BC\).
Lại có \(AO \bot AE\) (tính chất tiếp tuyến) nên \(AE{\rm{//}}BC\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.