Cho đoạn \[OO'\] và điểm \[A\] nằm trên đoạn \[OO'\] sao cho \[OA = 2O'A\]. Đường tròn \[(O)\] bán kính \[OA\] và đường tròn \[(O')\] bán kính \[O'A\]. Vị trí tương đối của hai đường tròn là:
A. Nằm ngoài nhau.
B. Cắt nhau.
C. Tiếp xúc ngoài.
D. Tiếp xúc trong.
Câu hỏi trong đề: 25 bài tập Vị trí tương đối của hai đường tròn có lời giải !!
Quảng cáo
Trả lời:
Chọn C
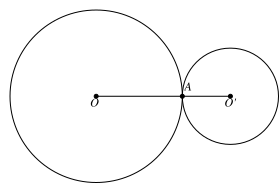
Vì hai đường tròn có một điểm chung là \[A\] và \[OO' = OA + O'A = R + r\] nên hai đường tròn tiếp xúc ngoài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. cắt nhau.
B. không giao nhau.
C. tiếp xúc trong.
D. tiếp xúc ngoài.
Lời giải
Chọn C
Ta có: \(R - r = 7 - 3 = 4\left( {cm} \right)\)
\[ \Rightarrow OO' = R - r\left( { = 4cm} \right)\]
Vậy hai đường tròn đã cho tiếp xúc trong.
Lời giải
Chọn A
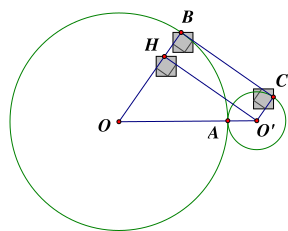
Kẻ \(O'H \bot OB\left( {H \in OB} \right)\).
Ta có \(BC\) là tiếp tuyến chung ngoài của \(\left( O \right)\) và \(\left( {O'} \right)\) \( \Rightarrow OB \bot BC;O'C \bot BC\).
\( \Rightarrow \) Tứ giác \(O'HBC\) là hình chữ nhật.
\[ \Rightarrow BC = HO'\] và \[HB = O'C = 1cm\].
\[ \Rightarrow OH = OB - HB = 4 - 1 = 3\left( {cm} \right)\]
Mà hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài nên \(OO' = OA + O'A = 4 + 1 = 5\left( {cm} \right)\)
Xét \(\Delta HOO'\left( {\widehat H = 90^\circ } \right):OO{'^2} = O{H^2} + HO{'^2}\)
\( \Rightarrow HO' = \sqrt {OO{'^2} - O{H^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\)
Vậy \(R \ge d \Leftrightarrow R \ge 2cm\).
Câu 3
A. \(4cm\).
B. \(3\sqrt 2 cm\).
C. \(6cm\).
D. \(5\sqrt 2 cm\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \({90^0}\)
B. \({60^0}\)
C. \({80^0}\)
D. \({100^0}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
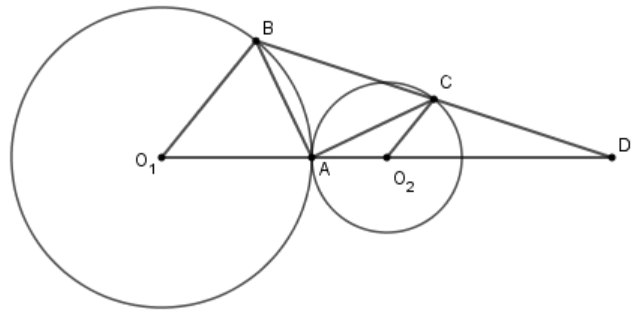
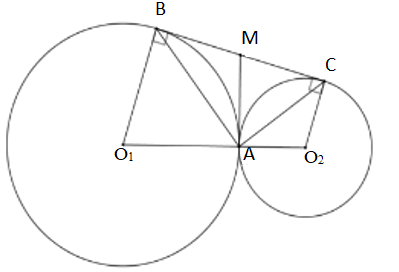
Câu 5
A. \(AM = \frac{{B{O_1} + C{O_2}}}{2}\)
B. \(AM \bot A{O_1};AM \bot A{O_2}\)
C. \(AM = \frac{1}{2}BC\)
D. \(AM = MC\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[OO' \approx 6,5cm\].
B. \[OO' \approx 6,1cm\].
C. \[OO' \approx 6cm\].
D. \[OO' \approx 6,2cm\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[{\rm{OO'}}\,\,{\rm{ < }}\,\,{\rm{7}}{\mathop{\rm cm}\nolimits} \].
B. \[{\rm{1cm}}\,\, \le \,\,{\rm{OO'}}\,\, \le \,\,{\rm{7}}{\mathop{\rm cm}\nolimits} \].
C. \[{\rm{OO'}}\,\, \ge \,1{\mathop{\rm cm}\nolimits} \].
D. \[{\rm{1cm}}\,\, < \,\,{\rm{OO'}}\,\,{\rm{ < }}\,\,{\rm{7}}{\mathop{\rm cm}\nolimits} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.