Cho hai đường tròn \[(O;10cm)\] và \[(O';5cm)\] cắt nhau tại \[A\] và \[B\]. Tính đoạn nối tâm \[OO'\], biết rằng \[AB = 8cm\] và \[O\] và \[O'\] nằm cùng phía đối với \[AB\]. (làm tròn đến chữ số thập phân thứ nhất).
Quảng cáo
Trả lời:
Chọn D
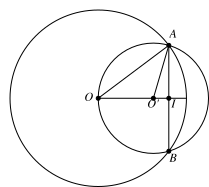
Ta có \[AI = \frac{1}{2}AB = 4\,cm\].
Theo định lý Phytagore ta có: \[O{I^2} = O{A^2} - A{I^2} = {10^2} - {4^2} = 84 \Rightarrow OI = 2\sqrt {21} \,cm\]
\[O'I = \sqrt {O'{A^2} - I{A^2}} = \sqrt {{5^2} - {4^2}} = 3\]
Do đó: \[OO' = OI - O'I = 2\sqrt {21} - 3 \approx 6,2(cm)\].
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn A
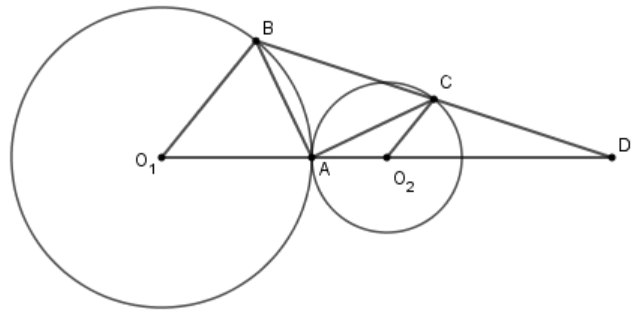
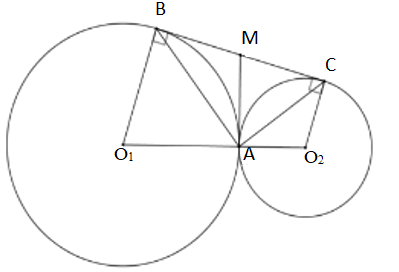
Xét \(({O_1})\)có \({O_1}B = {O_1}A\)\( \Rightarrow \Delta {O_1}AB\) cân tại \({O_1} \Rightarrow \widehat {{O_1}BA} = \widehat {{O_1}AB}\).
Xét \(({O_2})\)có \({O_2}C = {O_2}A\)\( \Rightarrow \Delta {O_2}CA\) cân tại \({O_2} \Rightarrow \widehat {{O_2}CA} = \widehat {{O_2}AC}\).
Lại có: \({O_1}B//{O_2}C\)
\( \Rightarrow \widehat {{O_1}BC} + \widehat {{O_2}CB} = {180^0}\)(hai góc trong cùng phía bù nhau)
Suy ra \(\widehat {{O_1}} + \widehat {{O_2}} = {360^0} - \widehat {{O_2}CB} - \widehat {{O_2}BC} = {180^0}\)
\( \Leftrightarrow {180^0} - \widehat {{O_1}BA} - \widehat {{O_1}AB} + {180^0} - \widehat {{O_2}CA} - \widehat {{O_2}AC} = {180^0}\)
\( \Leftrightarrow 2(\widehat {{O_1}AB} + \widehat {{O_2}AC}) = {180^0}\)
\( \Rightarrow \widehat {{O_1}AB} + \widehat {{O_2}AC} = {90^0} \Rightarrow \widehat {BAC} = {90^0}\)
Lời giải
Chọn C
Ta có: \(R - r = 7 - 3 = 4\left( {cm} \right)\)
\[ \Rightarrow OO' = R - r\left( { = 4cm} \right)\]
Vậy hai đường tròn đã cho tiếp xúc trong.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.