Tính góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) trong mỗi trường hợp sau:
a) \(d:\frac{{x + 2}}{2} = \frac{{y + 4}}{2} = \frac{{z + 1}}{1}\) và \((P):x + z + 24 = 0\);
b) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = - 1 + 2t}\\{z = - 2 - t}\end{array}} \right.\) và \((P):2x + 4y - 2z + 23 = 0\).
Tính góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) trong mỗi trường hợp sau:
a) \(d:\frac{{x + 2}}{2} = \frac{{y + 4}}{2} = \frac{{z + 1}}{1}\) và \((P):x + z + 24 = 0\);
b) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = - 1 + 2t}\\{z = - 2 - t}\end{array}} \right.\) và \((P):2x + 4y - 2z + 23 = 0\).
Quảng cáo
Trả lời:
a) Đường thẳng \(d\) có vectơ chỉ phương \(\vec a = (2;2;1)\). Mặt phẳng \((P)\) có vectơ pháp tuyến \(\vec n = (1;0;1)\).
Ta có \(\sin (d,(P)) = \frac{{|2.1 + 2.0 + 1.1|}}{{\sqrt {{2^2} + {2^2} + {1^2}} \cdot \sqrt {{1^2} + {0^2} + {1^2}} }} = \frac{1}{{\sqrt 2 }}\). Suy ra .
b) Đường thẳng \(d\) có vectơ chỉ phương \(\vec a = (1;2; - 1)\). Mặt phẳng \((P)\) có vectơ pháp tuyến \(\vec n = (2;4; - 2)\).
Ta có \(\sin (d,(P)) = \frac{{|1.2 + 2.4 + ( - 1) \cdot ( - 2)|}}{{\sqrt {{1^2} + {2^2} + {{( - 1)}^2}} \cdot \sqrt {{2^2} + {4^2} + {{( - 2)}^2}} }} = 1\). Suy ra .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
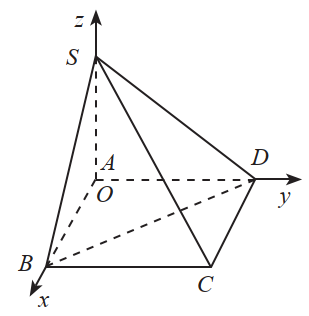
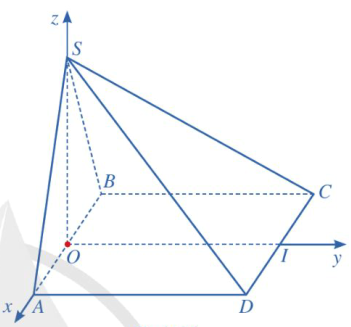
Trong không gian Oxyz, ta có \(C(2;3;0),\overrightarrow {SC} = (2;3; - 2)\); \(\overline {BD} = ( - 2;3;0)\).
a) Hai đường thằng SC và BD có vectơ chi phương lần lượt là \(\vec u = (2;3; - 2),\vec v = ( - 2;3;0)\).
Ta có \(\cos (SC,BD) = \frac{{|\vec u \cdot \vec v|}}{{|\vec u| \cdot |\vec v|}} = \frac{{|2 \cdot ( - 2) + 3 \cdot 3 + ( - 2) \cdot 0|}}{{\sqrt {{2^2} + {3^2} + {{( - 2)}^2}} \cdot \sqrt {{{( - 2)}^2} + {3^2} + {0^2}} }} = \frac{5}{{\sqrt {221} }}\).
Suy rab) Ta có phương trình mặt phẳng \((SBD)\) theo đoạn chắn là \(\frac{x}{2} + \frac{y}{3} + \frac{z}{2} = 1\) hay \(3x + 2y + 3z - 6 = 0\).
Mặt phẳng \((SBD)\) có vectơ pháp tuyến \(\vec n = (3;2;3)\), mặt đáy \((ABCD)\) có vectơ pháp tuyến \(\vec k = (0;0;1)\). Gọi \(\alpha \) là góc giũua mặt phẳng \((SBD)\) và mặt đáy.
Ta có \(\cos \alpha = \frac{{|\vec n \cdot \vec k|}}{{|\vec n| \cdot |\vec k|}} = \frac{{|3 \cdot 0 + 2 \cdot 0 + 3 \cdot 1|}}{{\sqrt {{3^2} + {2^2} + {3^2}} \cdot \sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{3}{{\sqrt {22} }}\). Suy rac) Gọi \(\beta \) là góc giũa đường thẳng SC và mặt phẳng \((SBD)\).
Ta có \(\sin \beta = \frac{{|\vec u \cdot \vec n|}}{{|\vec u| \cdot |\vec n|}} = \frac{{|2 \cdot 3 + 3 \cdot 2 + ( - 2) \cdot 3|}}{{\sqrt {{2^2} + {3^2} + {{( - 2)}^2}} \cdot \sqrt {{3^2} + {2^2} + {3^2}} }} = \frac{6}{{\sqrt {374} }}\). Suy raLời giải
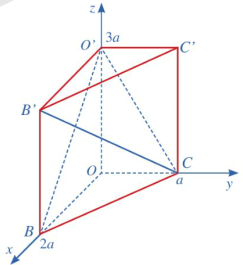
a) Ta có: \(\overrightarrow {B{B^\prime }} = \overrightarrow {O{O^\prime }} = (0;0;3a)\). Suy ra \({x_{{B^\prime }}} = {x_B} = 2a\), \({y_{{B^\prime }}} = {y_B} = 0,{z_{{B^\prime }}} - 0 = 3a\), tức là \({B^\prime }(2a;0;3a)\).
b) Vì \(B(2a;0;0),C(0;a;0),{O^\prime }(0;0;3a)\) nên mặt phẳng \(\left( {{O^\prime }BC} \right)\) có phương trình là
\(\frac{x}{{2a}} + \frac{y}{a} + \frac{z}{{3a}} = 1 \Leftrightarrow 3x + 6y + 2z - 6a = 0.\)
c) Mặt phẳng \(\left( {{O^\prime }BC} \right)\) có một vectơ pháp tuyến là \(\vec n = (3;6;2)\).
Do \({B^\prime }(2a;0;3a),C(0;a;0)\) nên \(\overrightarrow {{B^\prime }C} = ( - 2a;a; - 3a)\), suy ra vectơ \(\overrightarrow {{B^\prime }C} = ( - 2a;a; - 3a)\) cùng phương với vectơ \(\vec u = ( - 2;1; - 3)\). Vì thế vectơ \(\vec u = ( - 2;1; - 3)\) là một vectơ chỉ phương của đường thẳng \({B^\prime }C\). Suy ra sin của góc giữa đường thẳng \({B^\prime }C\) và mặt phẳng \(\left( {{O^\prime }BC} \right)\) bằng:
\(\frac{{|3 \cdot ( - 2) + 6 \cdot 1 + 2 \cdot ( - 3)|}}{{\sqrt {{3^2} + {6^2} + {2^2}} \cdot \sqrt {{{( - 2)}^2} + {1^2} + {{( - 3)}^2}} }} = \frac{6}{{7\sqrt {14} }} = \frac{{3\sqrt {14} }}{{49}}{\rm{. }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.