Bác Tùng gửi vào ngân hàng 200 triệu đồng theo thể thức lãi kép theo định kì với lãi suất không đổi \(x\) mỗi năm (tức là nếu đến kì hạn người gửi không rút lãi ra thì tiền lãi được tính vào tiền vốn của kì tiếp theo). Biểu thức \(S = 200{\left( {1 + x} \right)^3}\) (triệu đồng) là số tiền bác Tùng nhận được sau 3 năm.

a) Khai triển \(S\) thành đa thức ta được \(S = 200{x^3} + 600{x^2} + 600x + 200\).

b) Đa thức \(S = 200{\left( {1 + x} \right)^3}\) có bậc là 3.

c) Tổng số tiền bác Tùng nhận được sau 3 năm khi lãi suất \(x = 5\% \) lớn hơn \(230\) triệu đồng.

d) Số tiền lãi mà bác Tùng nhận được sau 3 năm là 30 triệu đồng.

Cho các số \(x,y,z \ne 0\) thỏa mãn đồng thời \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 2\) và \(\frac{2}{{xy}} - \frac{1}{{{z^2}}} = 4\). Tính giá trị của biểu thức \(P = {\left( {x + 2y + z} \right)^{2024}}\).

Từ một khối lập phương có cạnh bằng \(2x - 1{\rm{ }}\left( {{\rm{cm}}} \right)\), người ta cắt bỏ một khối lập phương có cạnh bằng \(2x - 3{\rm{ }}\left( {{\rm{cm}}} \right)\). Biết rằng thể tích còn lại của hình lập phương sau khi cắt là \(26{\rm{ c}}{{\rm{m}}^3}\).

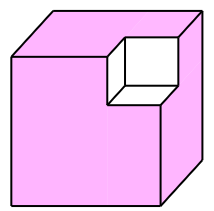
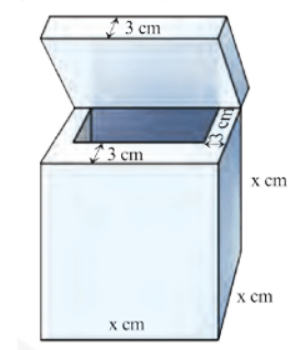
a) Thể tích của khối lập phương ban đầu là \({\left( {2x - 1} \right)^3}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)

b) Thể tích của khối hình lập phương bị cắt bỏ là \({\left( {2x - 3} \right)^3}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)

c) Đa thức biểu diễn phần thể tích còn lại sau khi cắt bỏ là \(24{x^2} - 48x + 26{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)

d) Độ dài của cạnh khối lập phương ban đầu là \(3{\rm{ }}\left( {{\rm{cm}}} \right).\)

Một mảnh đất hình vuông có cạnh là \(x{\rm{ }}\left( {\rm{m}} \right)\). Người ta mở rộng mảnh đất về bốn phía, mỗi phía \(2{\rm{ }}\left( {\rm{m}} \right)\) thì diện tích tăng thêm \(44{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

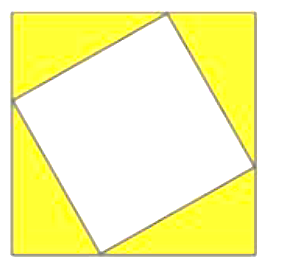
a) Diện tích ban đầu của mảnh đất hình vuông là \({x^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)

b) Diện tích của mảnh đất sau khi mở rộng là \({\left( {x + 2} \right)^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

c) Vì diện tích mảnh đất tăng thêm \(44{\rm{ }}\left( {{{\rm{m}}^2}} \right)\) nên ta có phương trình \({\left( {x + 2} \right)^2} - {x^2} = 44{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)

d) Diện tích ban đầu của mảnh đất lớn hơn \(12{\rm{ }}\left( {{{\rm{m}}^2}} \right).\)

Viết \(\left( {3x - 2} \right)\left( {9{x^2} + 6x + 4} \right)\) dưới dạng hiệu ta được:

Một người dùng các thanh kim loại để thiết kế một khung ảnh gồm hai hình vuông lồng vào nhau như hình vẽ dưới đây.

Trong đó, ảnh được gắn vào hình vuông nhỏ. Biết rằng tổng chiều dài của các thanh kim loại để làm khung là 168 cm và diện tích phần không gắn ảnh (phần tô màu) là 252 cm². Gọi \(x,y\) lần lượt là độ dài cạnh của hình vuông nhỏ và lớn \(\left( {x,y > 0,{\rm{ cm}}} \right)\).

a) Tổng chiều dài các thành kim loại làm khung là 168 cm nên \(4x + 4y = 168\).

b) Đa thức biểu diễn phần diện tích không gắn ảnh là \(S = {x^2} - {y^2}\).

c) Độ dài cạnh của hình vuông lớn là \(18\) cm.

d) Diện tích phần được gắn ảnh lớn hơn 300 cm².

Một thùng chứa dạng hình lập phương có độ dài cạnh bằng \(x\) (cm). Phần vỏ bao gồm nắp có độ dày 3 cm.

a) Phần lòng trong của thùng có độ dài cạnh là \(x - 6\) (cm).

b) Thể tích của thùng là \({x^3}\) (cm³).

c) Thể tích phần dung tích của thùng là \({\left( {x - 6} \right)^3}\) cm³.

d) Thể tích phần vỏ của thùng là \(18{x^2} + 108x + 216\) cm³.