Trong không gian với hệ tọa độ \(Oxyz\) cho đường thẳng \(d:\frac{{x - 5}}{2} = \frac{{y + 7}}{2} = \frac{{z - 12}}{{ - 1}}\) và mặt phẳng \(\left( \alpha  \right):x + 2y - 3z - 3 = 0\). Gọi \(M\) là giao điểm của \(d\) và \(\left( \alpha  \right)\), \(A\) thuộc \(d\) sao cho \(AM = \sqrt {14} \). Tính khoảng cách từ \(A\)đến mặt phẳng \(\left( \alpha  \right)\).

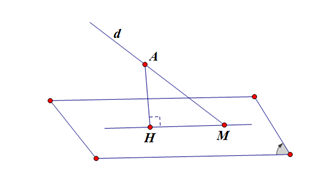
Đường thẳng \(d:\frac{{x - 5}}{2} = \frac{{y + 7}}{2} = \frac{{z - 12}}{{ - 1}}\) có một vectơ chỉ phương là \[\overrightarrow u  = \left( {2\,;\,2\,;\, - 1} \right)\].

Mặt phẳng \(\left( \alpha  \right):x + 2y - 3z - 3 = 0\)có một vectơ pháp tuyến là \[\overrightarrow n  = \left( {1\,;\,2\,;\, - 3} \right)\].

Ta có: \[\sin \left( {d\,;\,\left( \alpha  \right)} \right) = \frac{{\left| {\overrightarrow {{u_d}} \,.\,\overrightarrow {{n_\alpha }} } \right|}}{{\left| {\overrightarrow {{u_d}} } \right|\,.\,\left| {\overrightarrow {{n_\alpha }} } \right|}} = \frac{{3\sqrt {14} }}{{14}}\].

Gọi \[H\] là hình chiếu vuông góc của \(A\)lên mặt phẳng \(\left( \alpha  \right)\).

Khi đó tam giác \(\Delta MAH\) vuông tại \[H\] nên \[\sin \left( {d\,;\,\left( \alpha  \right)} \right) = \sin \widehat {AMH} = \frac{{AH}}{{AM}}\].

\[ \Rightarrow AH = AM\,.\,\sin \left( {d\,;\,\left( \alpha  \right)} \right) = 3\].

Vậy khoảng cách từ \(A\)đến mặt phẳng \(\left( \alpha  \right)\) bằng \(3\).