Tại cùng một thời điểm, có hai người đang ở hai vị trí \[A\] và \[B\] cách nhau \[1000\] mét. Người thứ nhất ở vị trí \[B\] và đi về phía điểm \[A\] với vận tốc \[2{\rm{\;m/s}}\] và người thứ hai ở vị trí \[A\] đi về phía điểm \[C\] với vận tốc \[1,5{\rm{\;m/s}}.\] Biết rằng \[AB\] và \[AC\] vuông góc với nhau. Hãy cho biết sau bao nhiêu giây thì khoảng cách giữa hai người này nhỏ nhất?
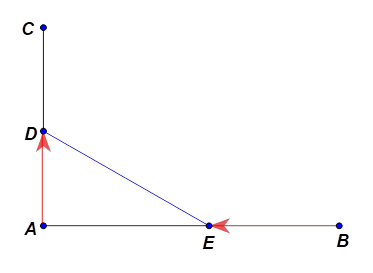
Tại cùng một thời điểm, có hai người đang ở hai vị trí \[A\] và \[B\] cách nhau \[1000\] mét. Người thứ nhất ở vị trí \[B\] và đi về phía điểm \[A\] với vận tốc \[2{\rm{\;m/s}}\] và người thứ hai ở vị trí \[A\] đi về phía điểm \[C\] với vận tốc \[1,5{\rm{\;m/s}}.\] Biết rằng \[AB\] và \[AC\] vuông góc với nhau. Hãy cho biết sau bao nhiêu giây thì khoảng cách giữa hai người này nhỏ nhất?
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 10 có đáp án !!
Quảng cáo
Trả lời:
Gọi \(x\) (giây) là thời gian di chuyển của mỗi người \(\left( {0 < x < 500} \right).\)
Quãng đường người thứ nhất đi được là: \(BE = 2x{\rm{\;(m)}}{\rm{.}}\)
Quãng đường người thứ hai đi được là: \(AD = 1,5x{\rm{\;(m)}}{\rm{.}}\)
Ta có \(AE = AB - BE = 1\,\,000 - 2x{\rm{\;(m)}}{\rm{.}}\)
Khoảng cách giữa hai người là nhỏ nhất khi DE ngắn nhất.
Xét \(\Delta ADE\) vuông tại \(A,\) theo định lí Pythagore, ta có:
\(D{E^2} = A{D^2} + A{E^2} = {\left( {1,5x} \right)^2} + {\left( {1\,\,000 - 2x} \right)^2} = 2,25{x^2} + 4{x^2} - 4\,\,000x + 1\,\,000\,\,000\)
\( = 6,25{x^2} - 4\,\,000x + 1\,\,000\,\,000 = 6,25\left( {{x^2} - 640x + 102\,\,400} \right) + 360\,\,000\)
\( = 6,25{\left( {x - 320} \right)^2} + 360\,\,000.\)
Ta có: \({\left( {x - 320} \right)^2} \ge 0\) với mọi \(x\) nên \(6,25{\left( {x - 320} \right)^2} + 360\,\,000 \ge 360\,\,000.\)
Do đó \(D{E^2} \ge 360\,\,000\) nên \(DE \ge 600\).
Dấu “=” xảy ra khi \[{\left( {x - 320} \right)^2} = 0\] hay \(x = 320.\)
Vậy sau \[320\] giây thì khoảng cách giữa hai người là nhỏ nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi vận tốc của xe tải là \[x\] km/h (điều kiện \(x > 0).\)
Vận tốc của xe con là \(x + 10\) (km/h).
Thời gian đi từ \[A\] đến \[B\] của xe tải, xe con lần lượt là \(\frac{{200}}{x}\) giờ và \(\frac{{200}}{{x + 10}}\) giờ.
Vì xe tải xuất phát trước xe con 40 phút \( = \frac{2}{3}\) giờ và hai xe đến \[B\] cùng lúc nên ta có phương trình \(\frac{{200}}{x} - \frac{{200}}{{x + 10}} = \frac{2}{3}\).
Giải phương trình:
\(\frac{{200}}{x} - \frac{{200}}{{x + 10}} = \frac{2}{3}\)
\(\frac{{200\left( {x + 10} \right) - 200x}}{{x\left( {x + 10} \right)}} = \frac{2}{3}\)
\(\frac{{200x + 2\,\,000 - 200x}}{{x\left( {x + 10} \right)}} = \frac{2}{3}\)
\(\frac{{2\,\,000}}{{x\left( {x + 10} \right)}} = \frac{2}{3}\)
\(2x\left( {x + 10} \right) = 3 \cdot 2\,\,000\)
\({x^2} + 10x - 3000 = 0.\)
Giải phương trình được \({x_1} = - 60\) (không thỏa mãn), \({x_2} = 50\)(thỏa mãn).
Thời gian xe tải đi từ \[A\] đến \[B\] là \(\frac{{200}}{{50}} = 4\) giờ.
Vậy hai xe đến \[B\] lúc 12 giờ.
Đáp án: 12.
Lời giải
Độ dài dây \(AB\) nhỏ nhất khi \(A\) và \(B\) có vị trí như hình vẽ.
Xét \(\Delta ABH\) vuông tại \(H\), ta có: \[HB = AB \cdot \sin \widehat {BAH}\].
Suy ra \[AB = \frac{{HB}}{{\sin \widehat {BAH}}} \approx \frac{{3,146}}{{\sin 4^\circ }} \approx 45,1{\rm{\;(m)}}{\rm{.}}\]
Vậy độ dài dây \(AB\) nhỏ nhất khoảng \(45,1{\rm{\;m}}.\)
Đáp án: 45,1.
Câu 3
A. \(\left[ { - 3;1} \right]\).
B. \(\left\{ { - 3;1} \right\}\).
C. \(\left[ { - 3;1} \right)\).
D. \(\left( { - 3;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 13 cm.
B. \(\frac{{13}}{2}\;{\rm{cm}}\).
C. \(\frac{{13\sqrt 2 }}{2}\;{\rm{cm}}\).
D. \(\frac{{5\sqrt 2 }}{2}\;{\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
