Cho hàm số f(x) có đạo hàm là f'(x) =3x2 + ex. Giá trị lớn nhất của hàm số f(x) trên [0; 2] là:
A. f(2).
B. f(0).
C. f(1).
D. 12 + e2.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
Ta có f'(x) = 3x2 + ex > 0, ∀x Î [0; 2].
Do đó hàm số y = f(x) đồng biến trên [0; 2].
Do đó giá trị lớn nhất của hàm số f(x) trên [0; 2] là f(2).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức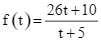 
(f(t) được tính bằng nghìn người) (Nguồn : Giải tích 12 nâng cao, NXBGD Việt Nam, 2020). Xem y = f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Đồ thị hàm số y = f(t) có đường tiệm cận ngang là y = a. Giá trị của a là bao nhiêu ?
(f(t) được tính bằng nghìn người) (Nguồn : Giải tích 12 nâng cao, NXBGD Việt Nam, 2020). Xem y = f(t) là một hàm số xác định trên nửa khoảng [0; +∞). Đồ thị hàm số y = f(t) có đường tiệm cận ngang là y = a. Giá trị của a là bao nhiêu ? Lời giải
Ta có 
; 
nên y = 26 là tiệm cận ngang của đồ thị hàm số.
Do đó a = 26.
Trả lời: 26.
Lời giải
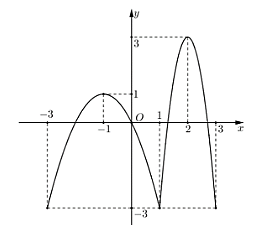
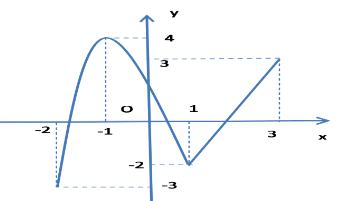
Từ đồ thị hàm số y = f'(x) ta lập bảng biến thiên của hàm số y = f(x) trên đoạn [−1; 1] như sau
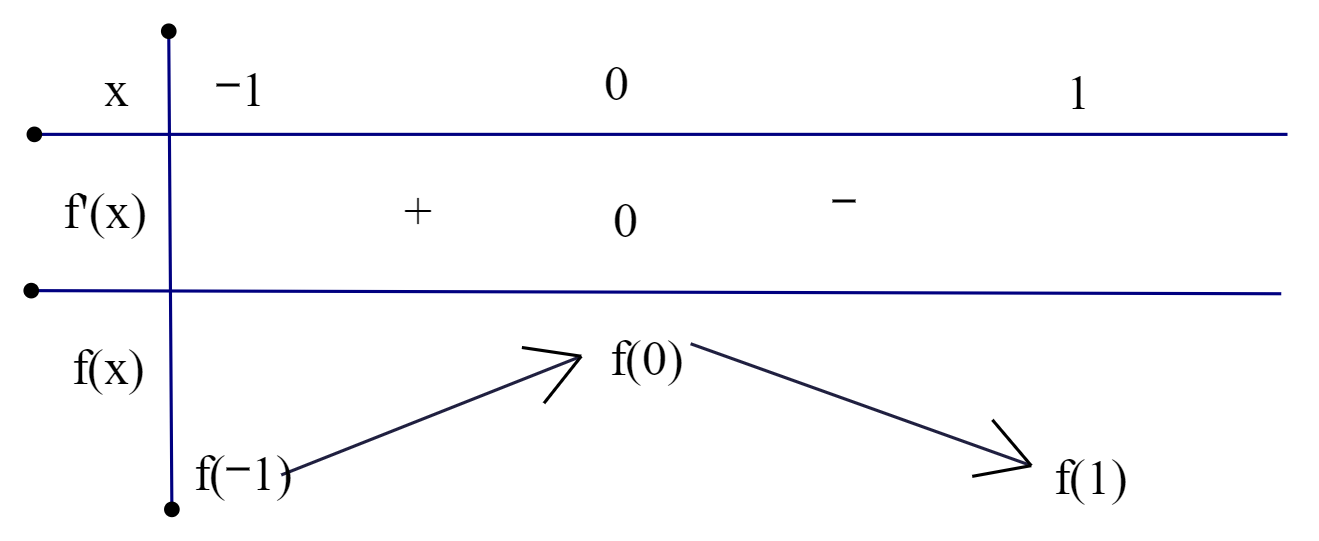
Dựa vào bảng biến thiên ta có 
.
Do đó x0 = 0.
Trả lời: 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập