PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm giá trị nhỏ nhất của hàm số \(f(x) = \frac{{{x^2} + 9}}{x}\) trên khoảng \((0; + \infty )\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm giá trị nhỏ nhất của hàm số \(f(x) = \frac{{{x^2} + 9}}{x}\) trên khoảng \((0; + \infty )\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp số: 6
Xét hàm số \(f(x) = \frac{{{x^2} + 9}}{x}\) với \(x \in (0; + \infty )\).
Ta có: \(f'(x) = \frac{{{x^2} - 9}}{{{x^2}}}\). Khi đó, \(f'(x) = 0 \Leftrightarrow x = 3\) (do \(\left. {x > 0} \right)\).
Ngoài ra \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
Bảng biến thiên của hàm số như sau:
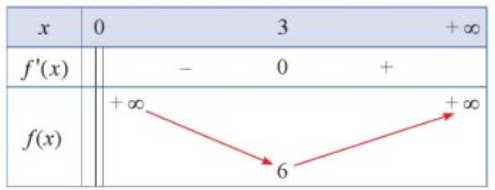
Căn cứ bảng biến thiên, ta có: \(\mathop {\min }\limits_{(0; + \infty )} f(x) = 6\) tại \(x = 3\) và hàm số \(f(x)\) không có giá trị lớn nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \[\left[ {1\,;\,3} \right]\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759147890.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
Dựa vào đồ thị hàm số suy ra
a) \(m = - 4\).
b) \(M = 0\).
c)\(M + m = 0 + ( - 4) = - 4\).
d) Với \(\forall x \in \left[ { - 1\,;\, + \infty } \right)\), ta có: \(f\left( x \right) \le 0 \Rightarrow f\left( x \right) + 4 \le 4\) và \(f\left( x \right) + 4 = 4 \Leftrightarrow f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right.\)
Vậy, giá trị lớn nhất của hàm số \(y = f\left( x \right) + 4\) trên nửa khoảng \(\left[ { - 1\,;\, + \infty } \right)\) là \(4\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
TXĐ: \[D = \mathbb{R}\]
Có \( - 1 \le \sin 2025x \le 1 \Leftrightarrow - 3 \le 3\sin 2025x \le 3 \Leftrightarrow 2 \le 3\sin 2025x + 5 \le 8\)
Suy ra: \(\mathop {{\rm{max}}}\limits_\mathbb{R} y = 8 \Leftrightarrow \sin 2025x = 1 \Leftrightarrow x = \frac{\pi }{{4050}} + \frac{{k2\pi }}{{2025}}\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập