Một đường tròn có bán kính \(R = 12cm\). Tính độ dài của cung \({60^0}\) trên đường tròn gần bằng
Quảng cáo
Trả lời:
Chọn D
Ta có \({60^0}\)tương ứng với góc \(\frac{\pi }{3}rad\). Do đó độ dài cung tròn là \(l = R\alpha = 12.\frac{\pi }{3} = 4\pi = 12,56cm\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bán kính đường tròn là \(R = \frac{{60}}{2} = 30\;cm\).
a) Ta có: ; suy ra độ dài cung nhỏ \(AB\) là .
b) Ta có: ; suy ra độ dài cung nhỏ \(AC\) là
Lời giải
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
a) Ta có: \[(OA,OB) = \frac{\pi }{4} + k2\pi (k \in \mathbb{Z})\];
b) Ta thấy \(A,C,E,G\) lần lượt biểu diễn cho các góc lượng giác \(0rad,\frac{\pi }{2}rad,\pi rad,\frac{{3\pi }}{2}rad,2\pi rad\), \(\frac{{5\pi }}{2}{\mathop{\rm rad}\nolimits} ,..\). Tất cả các góc này theo thứ tự chênh lệch nhau \(\frac{\pi }{2}\) rad. Vì vậy công thức duy nhất biểu diễn cho các góc lượng giác ấy là \(k\frac{\pi }{2}(k \in \mathbb{Z})\).
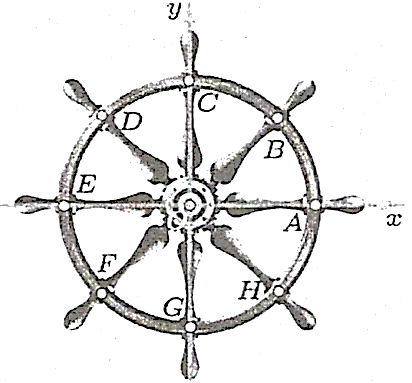
c) Ta thấy hai điểm \(A,E\) lần lượt biểu diễn cho các góc lượng giác Tất cả các góc này theo thứ tự chênh lệch nhau \({180^^\circ }\). Vì vậy công thức duy nhất biểu diễn cho các góc lượng giác ấy là
d) Theo hệ thức Sa-lơ, ta có:
\(\begin{array}{l}(OA,OB) + (OB,OC) = (OA,OC) = \frac{\pi }{2} + k2\pi (k \in \mathbb{Z})\\(OA,OC) + (OC,OH) = (OA,OH) = - \frac{\pi }{4} + k2\pi (k \in \mathbb{Z})\end{array}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
